Auf dieser Seite wird euch gezeigt, wie man den Abstand zwischen zwei Punkten berechnet. Im ersten Teil geht es um Punkte in der Ebene und im zweiten Teil um den Abstand zweier Punkte im Raum.
Abstand zwischen zwei Punkten der Ebene
Zwei Punkte P(xP , yP) und Q(xQ , yQ) der Ebene haben den Abstand
![]()
An der Grafik kann man erkennen, dass sich diese Formel für den Abstand aus dem Satz des Pythagoras ergibt:
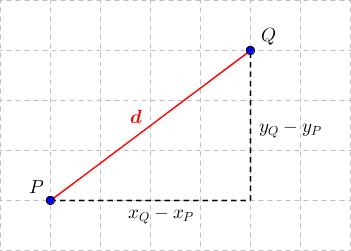
Abstand zweier Punkte in der Ebene
Beispiel:
Zu bestimmen ist der Abstand zwischen den beiden Punkten P(2 , 2) und Q(6 , 5). Der Abstand d beträgt
d = Wurzel aus[ (6-2)2 + (5-2)2 ] = Wurzel aus[16 + 9] = 5 .
Abstand zwischen zwei Punkten des Raumes
Zwei Punkte P(xP , yP , zP) und Q(xQ , yQ , zQ) des Raumes haben den Abstand
![]()
Man kann den Abstand zwischen zwei solchen Punkten als die Länge der Raumdiagonale in einem Quader auffassen. Wie die Grafik zeigt, ergibt sich dann die Berechnungsformel durch zweimaliges Anwenden des Satz des Pythagoras:
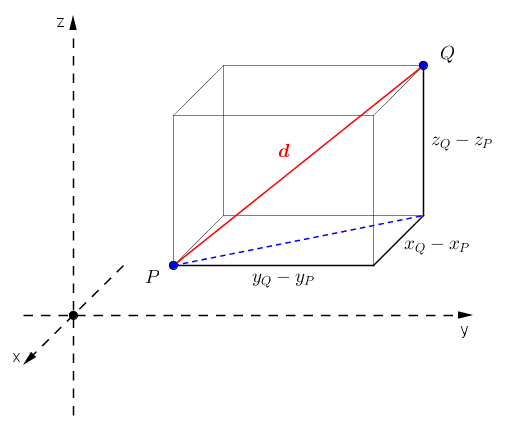
Abstand zweier Punkte im Raum
Beispiel:
Zu bestimmen ist der Abstand zwischen den beiden Punkten P(2 , 2 , 2) und Q(-2 , 6 , 5). Der Abstand d beträgt
d = Wurzel aus[ (-2-2)2 + (6-2)2 + (5-2)2 ] = Wurzel aus[16 + 16 + 9] = 6,4031 .