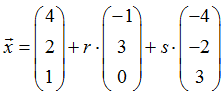Drei Punkte Gleichung einer Ebene
Ebenen im dreidimensionalen Raum können durch eine sogenannte Dreipunktegleichung einer Ebene dargestellt werden.
Drei Punkte Gleichung einer Ebene

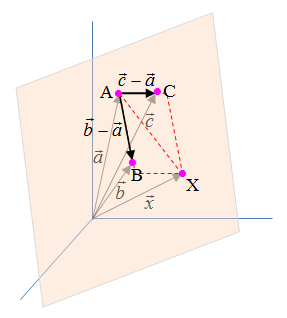
Voraussetzung für diese Art der Darstellung einer Ebene ist, dass die drei Punkte A, B, C nicht auf einer Geraden liegen.
Natürlich ist diese Darstellungsart identisch mit einer Parametergleichung, da man ja aus den ursprünglichen Punkten die beiden Richtungsvektoren →
b–→
a und →
c–→
a bildet und den Ortsvektor von Punkt A als Stützvektor verwendet.
Beispiel:
Zu bestimmen ist die Dreipunktegleichung der Ebene E, welche durch die drei Punkte A(4; 2; 1), B(3; 5; 1) und C(0; 0; 4) festgelegt ist.
Aus den drei Punkten erhalten wir die drei Vektoren
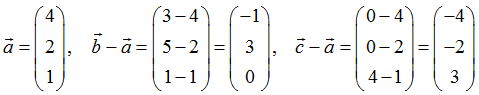
Die Dreipunktegleichung der Ebene lautet somit