Normalengleichung einer Ebene
Die Lage einer Ebene im dreidimensionalen Raum kann durch eine Normalengleichung der Ebene, auch Normalenform genannt, dargestellt werden.
Normalengleichung einer Ebene

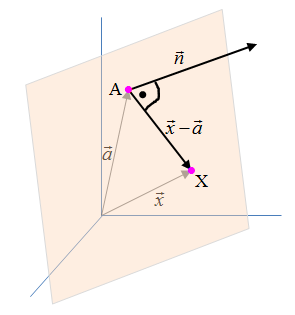
Voraussetzung für diese Art der Darstellung einer Ebene E ist, dass der Vektor →
n ≠ 0 senkrecht zur Ebene E verläuft, dass also das Skalarprodukt →
AX · →
n für jeden Punkt X der Ebene gleich Null ist.
Beispiel:
Eine Ebene E ist gegeben durch die folgende Normalengleichung
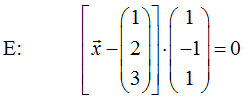
Hier wird der Stützvektor aus dem Punkt A(1; 2; 3) gebildet und als Normalenvektor ein beliebiger von 0 verschiedener Vektor verwendet. Mit einem Computerprogramm gezeichnet, sieht das Ganze so aus:
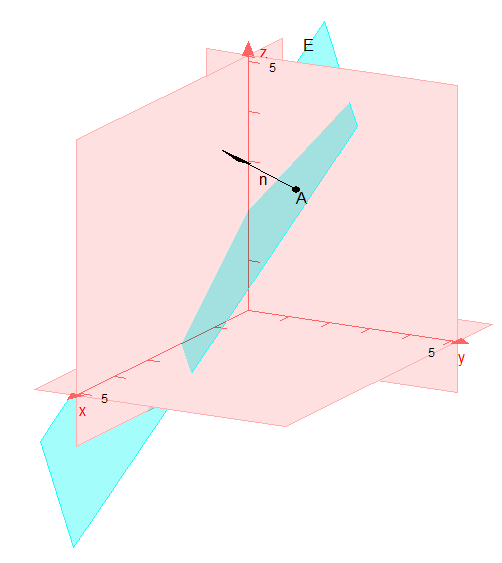
Die Normalengleichung lässt sich noch etwas vereinfachen:
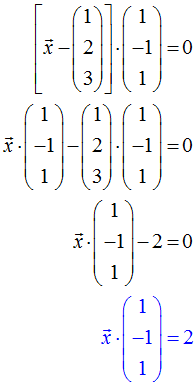
Man nennt diese Vereinfachung (blaue Gleichung) die vereinfachte Normalengleichung bzw. vereinfachte Normalenform der Ebene.