Parametergleichung in Normalengleichung
Von der Parametergleichung zur Normalengleichung: In diesem Beitrag wird an einem Beispiel gezeigt, wie sich eine Ebene in Parametergleichung / Punktrichtungsform in eine Normalengleichung / Normalenform umwandeln lässt.
Die Aufgabe besteht also darin, eine Parametergleichung
![]()
einer Ebene in eine Normalengleichung
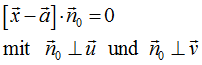
umzuwandeln.
Den Stützvektor →
a aus der gegeben Parametergleichung können wir direkt in die Normalengleichung übernehmen. Der Normalenvektor →
n0 muss senkrecht zur Ebene, also senkrecht zu den beiden Richtungsvektoren →
u und →
v aus der Parametergleichung stehen.
Betrachten wir als Beispiel die folgende Parametergleichung
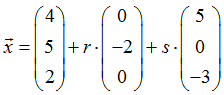
In einem ersten Schritt übertragen wir den Stützvektor, der ja für einen Punkt aus der Ebene steht, in die Normalengleichung und gelangen damit zunächst zur folgenden Darstellung
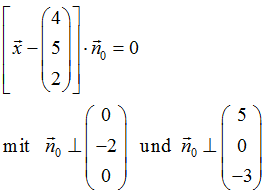
Das der Normalenvektor →
n0 senkrecht zu den beiden Richtungsvektoren verläuft, bedeutet natürlich, dass das Skalarprodukt von →
n0 mit den beiden Richtungsvektoren jeweils Null ergibt. Beschreiben wir den Normalenvektor durch die drei Koordinaten x, y, z führt das auf diese beiden Gleichungen
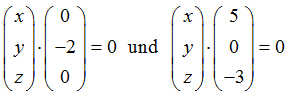
Rechnen wir die Skalarprodukte aus und schreiben die Gleichungen untereinander, so ergibt das ein Gleichungssystem aus zwei Gleichungen mit drei Unbekannten
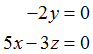
Die erste Gleichung ergibt notwendig y = 0. Die zweite Gleichung hat mehr als eine Lösung. Da wir nur eine benötigen, können wir einen der beiden Parameter – entweder x oder z frei wählen. Wählen wir z.B. z = 5 so ist zwangsläufig x = 3.
Damit ist also
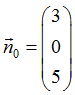
ein möglicher Normalenvektor (eine Probe würde schnell bestätigen, dass die entsprechenden Skalarprodukte mit den beiden Richtungsvektoren aus der Parametergleichung jeweils Null ergeben).
Tipp: Man kann natürlich auch einen Normalenvektor von Hand oder mit einem Taschenrechner berechnen, indem man das Kreuzprodukt (Vektorprodukt) →
u x →
v der beiden Richtungsvektoren bildet.
Insgesamt erhaltet wir somit die folgende Normalenform für die vorliegende Ebene
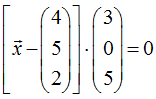
Man mache sich klar, dass es unendlich viele äquivalente Normalengleichungen für ein und dieselbe Ebene gibt – man braucht ja dafür bloß einen Punkt aus der Ebene (wovon es unendlich viele gibt) und einen zur Ebene senkrechten Vektor (auch davon gibt es unendlich viele)!