Dieser Beitrag erklärt die vektorielle Parametergleichung einer Geraden. Mit Hilfe eines Stützvektors und eines Richtungsvektors erhält man diese Darstellung einer Geraden im Raum.
Die vektorielle Parametergleichung einer Geraden g lautet
Vektor 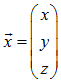 repräsentiert einen laufenden Punkt auf der Geraden, repräsentiert einen laufenden Punkt auf der Geraden, |
Vektor 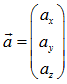 ist der Stützvektor, ist der Stützvektor, |
Vektor 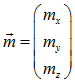 ist der Richtungsvektor und muss vom Nullvektor verschieden sein, ist der Richtungsvektor und muss vom Nullvektor verschieden sein, |
Das folgende Bild veranschaulicht diese Darstellungsart einer Geraden:
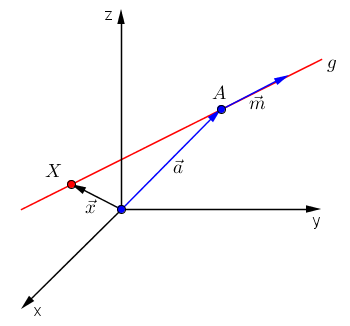
Vektorielle Parametergleichung einer Geraden
Beispiel:
Zu bestimmen ist die Gleichung einer Geraden g durch den Punkt A = (1 ; 2 ; 3) in Richtung des Vektors 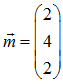 . Man erhält
. Man erhält
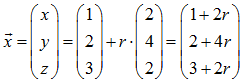
Beispiel:
Für welchen Parameter r liegt der Punkt X = (13 ; 8 ; 6) auf der Geraden
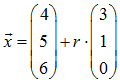
Es ist 13 = 4 + r · 3, also r = 3.
Analog erhält man aus 8 = 5 + r · 1
und aus 6 = 6 + r · 0
für den Parameter r den Wert 3.