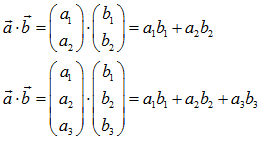Skalarprodukt von Vektoren

In diesem Beitrag geht es um das Skalarprodukt von Vektoren, wie ist es definiert, wie kann man es berechnen und wie kann man es in Code umsetzen.

Für zwei Vektoren $\vec{a}, \vec{b}$ definiert man das Skalarprodukt dieser beiden Vektoren durch

$\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos\gamma$
wobei 0°≤γ≤180°.

Hier ist $|\vec{a}|$ der Betrag von Vektor $\vec{a}$ ,

$|\vec{b}|$ der Betrag von Vektor $\vec{b}$ und

γ der (kleinere) Winkel zwischen beiden Vektoren.

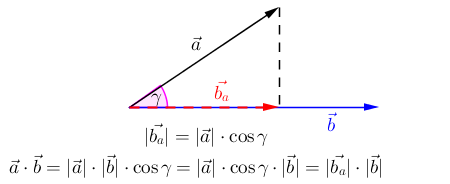
Skalarprodukt von Vektoren

An der Zeichnung erkennt man gut, dass das Skalarprodukt der Vektoren $\vec{a}, \vec{b}$ nichts Anderes ist, als das Produkt aus der Länge des rot-gestrichelten Vektors $\vec{b_a}$ und der Länge des blauen Vektors $\vec{b}$ .

Diesen Zusammenhang kennt man aus der Physik:

Arbeit = Kraft in Wegrichtung · Weglänge

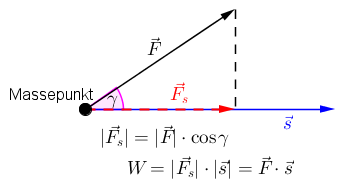
Arbeit W als Skalarprodukt aus Kraftvektor und Wegvektor

Da man Vektoren der Ebene bzw. des Raums in Form von Spaltenvektoren mit 2 bzw. 3 Koordinaten darstellen kann, gibt es natürlich auch eine Koordinatenform des Skalarproduktes $\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos\gamma$

Koordinatenform des Skalarproduktes:

Beispiele:

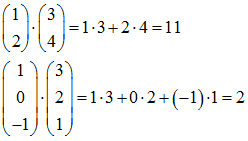
Die Berechnung von Skalarprodukten lässt sich kinderleicht in Code umsetzen, wie dieses JavaScript-Beispiel zeigt:

Rechen-Fuchs

Skalarprodukt von Vektoren

Auch interessant: