Dieser Beitrag erklärt euch die Definition der Ableitungsfunktion, wie man eine Ableitungsfunktion berechnen kann und wie man sie (ohne vorher zu berechnen) zeichnen kann.
Definition der Ableitungsfunktion
Ist f eine Funktion mit Definitionsbereich D, Wertebereich W und D´ = {x ∈ D | f´(x) existiert }, dann nennt man
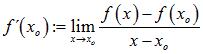
die Ableitungsfunktion von f.
Die Ableitungsfunktion ordnet also jeder Stelle xo den Anstieg mo = f´(xo) des Funktionsgraphen an dieser Stelle zu (sofern er existiert).
Es sei ausdrücklich darauf hingewiesen, dass D und D´ verschieden sein können! So ist z.B. die Wurzelfunktion für alle reellen x ≥ 0 definiert, ihre Ableitung dagegen für alle reellen x > 0:
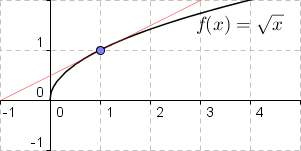 |
Definitionsbereich: x ≥ 0 |
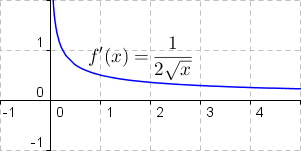 |
Definitionsbereich: x > 0 der Grenzwert 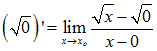 extistiert nicht! extistiert nicht! |
Ableitungsfunktion berechnen
Man berechnet zu einer gegebenen Funktion f deren Ableitungsfunktion f´, indem man formal den Grenwert f´(xo) für eine Variable xo berechnet. Dabei muss man bei Umformungen und Grenzwertbetrachtungen natürlich berücksichtigen, ob es irgendwelche Einschränkungen für xo gibt.
Das folgende Beispiel führt eine solche formale Grenzwertberechnung mit der Wurzelfunktion durch. Am Ende stellt sich heraus (s. Grafik oben), dass der so gefundene Grenzwert nur für x > 0 existiert:
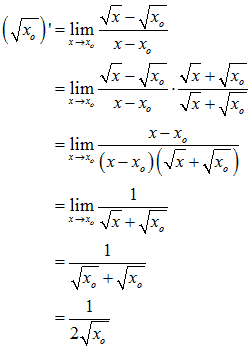
Ableitungsfunktion zeichnen
Hat man zu einer gegebenen Funktion f die Ableitungsfunktion f´ schon berechnet, so ist das Zeichnen in der Regel kein Problem. Will oder kann man aus irgendwelchen Gründen die Ableitungsfunktion nicht berechnen, so kann man sich ihren Graphen trotzdem (zumindest näherungsweise) aus dem Graphen der vorgelegten Funktion f herleiten. Dies nennt man auch graphisches Ableiten oder graphisches Differenzieren.
Beim graphischen Ableiten kann man folgendermaßen vorgehen:
- Man markiere Punkte (x1, y1), (x2, y2), … , (xn, yn) auf dem Graphen von f.
- Nun ermittle man näherungsweise die Anstiege m1, m2, … , mn in diesen Punkten – z.B. duch kleine Steigungsdreiecke und der Berechnung des entsprechenden Anstiegs m = Δy/Δx
- Man trage nun die Punkte (x1, m1), (x2, m2), … , (xn, mn) ebenfalls in das Koordinatensystem ein. Jetzt verbindet man diese möglichst glatt miteinander und erhält so eine Näherung für den tatsächlichen Graphen der Ableitungsfunktion f´.
Von der Homepage des Cornelsen-Verlags stammt diese schöne und anschauliche Anleitung für graphisches Ableiten mit Hilfe eines kleinen Spiegels.
