Auf dieser Seite wird erklärt, was eine abzählbare Menge ist.
Abzählbare Menge
Eine Menge M heißt abzählbar, wenn einer der folgenden Bedingungen erfüllt ist:
- Die Menge M enthält höchstens endlich viele Elemente.
- Die Menge M enthält unendlich viele Elemente und es gibt eine bijektive Abbildung
ν : M → IN.
Die Abbildung in der zweiten Bedingung nennt man eine Abzählung oder Nummerierung.
Nach Bedingung 2. ist eine unendliche Menge abzählbar, wenn sie gleichmächtig zur Menge der Natürlichen Zahlen ist.
Beispiele für abzählbare Mengen:
Die Leere Menge {}, die Ganzen Zahlen IZ, die Rationalen Zahlen IQ, die Mengen IN2, IN3 (allgemein INn, n∈IN) sind alles abzählbare Mengen.
Nummerierung von IN2
Die Cantorsche Paarungsfunktion π : IN2 → IN ist ein Beispiel für eine Nummerierung der Menge IN2. Sie ist folgendermaßen definiert:
Der Grafik unten kann man die Technik der Abzählung entnehmen:
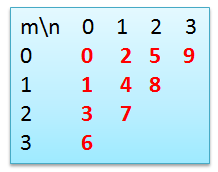
π(0,0) = 0
π(1,0) = 1 , π(0,1) = 2
π(2,0) = 3 , π(1,1) = 4 , π(0,2) = 5
π(3,0) = 6 , π(2,1) = 7 , π(1,2) = 8 , π(0,3) = 9
usw.