In diesem Beitrag geht es darum, mit Mitteln der Analytischen Geometrie die Seitenhalbierenden in einem Dreieck und deren Schnittpunkt zu untersuchen.
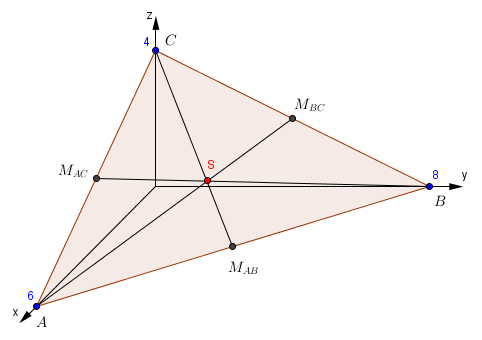
Die Seitenhalbierenden eines jeden Dreiecks schneiden sich in einem gemeinsamen Punkt S. Wir wollen den Schnittpunkt des unten dargestellten Dreiecks berechnen und rechnerisch bestätigen, dass er auf allen drei Seitenhalbierenden liegt: