Chi Quadrat Verteilung

Jede Zufallsvariable der Form

Χ2 = X12 + X22 + … + Xn2

mit unabhängigen Zufallsvariablen X1, X2, … , Xn, die alle Normalverteilt mit Mittelwert 0 und Varianz 1 sind, unterliegt einer sogenannten
Chi Quadrat Verteilung (χ2-Verteilung) mit n Freiheitsgraden.

Dichte der Chi Quadrat Verteilung für n=3 Freiheitsgrade

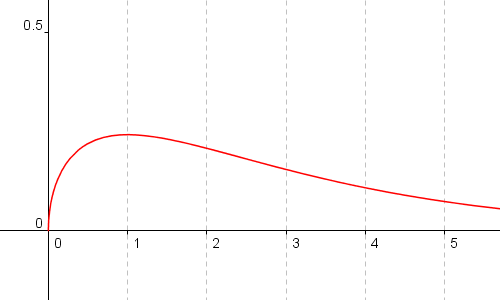
Dichte der Chi Quadrat Verteilung für n=3 Freiheitsgrade

 
Die Dichte der Chi Quadrat Verteilung ist

f(x) = \cfrac{1}{2^{n/2} \Gamma(n/2)} x^{(n-2)/2} e^{-x/2} für x>0
f(x) = 0 für x\le0

und die Verteilungsfunktion der Chi Quadrat Verteilung lautet

F(x) = \cfrac{1}{2^{n/2} \Gamma(n/2)} \int\limits_0^x t^{(n-2)/2} e^{-t/2} dt

\Gamma(n/2) ist der Funktionswert der sogenannten Gammafunktion für das Argument n/2.

Der Erwartungswert einer Chi Quadrat Verteilung mit n Freiheitsgraden ist n und ihre Varianz ist 2n.

Auch interessant: