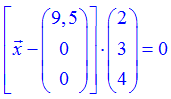Koordinatengleichung in Normalengleichung
Auf dieser Seite geht es darum, wie sich eine gegebene Koordinatengleichung einer Ebene in eine Normalengleichung dieser Ebene umwandeln lässt.
Sei also die folgende Ebene E in Koordinatenform gegeben
![]()
Eine Normalengleichung hat die Form
![]()
mit einem Ortsvektor →
a eines Punktes A, der in der Ebene liegt und einem Normalenvektor →
n, der senkrecht zur Ebene verläuft.
Den Normalenvektor →
n können wir direkt aus der Koordinatengleichung ablesen. Er entspricht nämlich den drei Koeffizienten von x, y und z
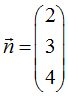
Damit haben wir zunächsteinmal die vereinfachte Form der Normalengleichung
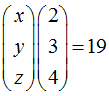
bzw.
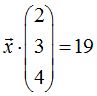
Was uns nun noch fehlt, ist der Ortsvektor eines Punktes A der Ebene. Dazu setzen wir y = z = 0 in die gegebene Koordinatengleichung ein und erhalten
bzw. x = 9,5
und somit den Punkt A(9,5 ; 0; 0) mit seinem Ortsvektor
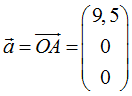
Jetzt sind alle Bausteine für die gesuchte Normalengleichung zusammengetragen und sie lautet