In diesem Beitrag geht es um die Funktionen vom Typ y = a · sin(x), insbesondere um den Einfluss des Parameters a.
Definitionsbereich
Der Definitionsbereich umfasst die gesamten reellen Zahlen -∞ < x < ∞, ist also genau der Gleiche, wie bei der herkömmlichen Sinusfunktion.
Wertebereich
Der Wertebereich umfasst alle reellen Zahlen im Intervall -|a| ≤ y ≤ |a|, denn die Werte der Funktionen y = a · sin(x) entstehen aus denen der Sinusfunktion sin(x) durch Multiplikation mit dem Faktor a.
Der Parameter a beeinflusst damit das entsprechende Aussehen der Graphen:
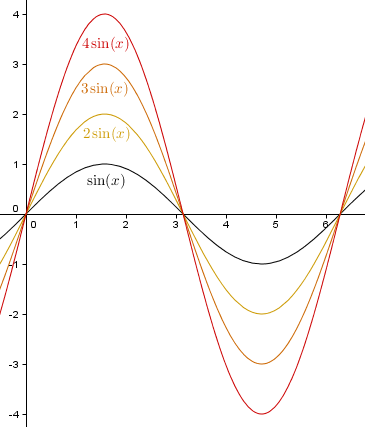
a > 1
Die ursprüngliche Sinuskurve wird in Richtung der y-Achse gedehnt:
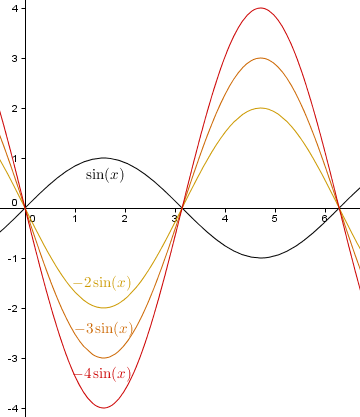
a < -1
Die ursprüngliche Sinuskurve wird in Richtung der y-Achse gedehnt und an der x-Achse gespiegelt:
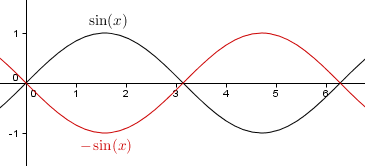
a = -1
Die ursprüngliche Sinuskurve wird an der x-Achse gespiegelt:
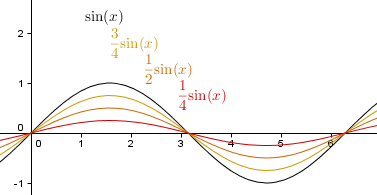
0 < a < 1
Die ursprüngliche Sinuskurve wird in Richtung der y-Achse gestaucht:
-1 < a < 0
Die ursprüngliche Sinuskurve wird in Richtung der y-Achse gestaucht und an der x-Achse gespiegelt:
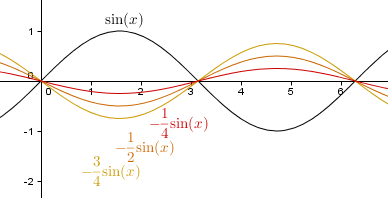
Wie man den verschiedenen Graphen entnehmen kann, hat der Parameter a keinen Einfluss auf die Periode oder die Nullstellen der Funktionen y = a · sin(x) im Vergleich zur Sinusfunktion y = sin(x).