Auf dieser Seite wird euch erklärt, wie man die graphische Lösung einer linearen Gleichung mit einer Variablen bestimmt.
Beschreibung der Methode
Jede lineare Gleichung mit einer Variablen (Unbekannten), wie zum Beispiel 7x-21=14, lässt sich durch Äquivalenzumformungen auf die Form
bringen.
Die Lösung dieser Gleichung ist nichts anderes als die Nullstelle der Funktion y = ax + b.
Um nun die graphische Lösung der Gleichung ax + b = 0 zu gewinnen, zeichnet man den Graphen der Funktion y = ax + b und liest die Nullstelle aus der Zeichnung ab.
Aufgrund der Ungenauigkeiten beim Zeichnen ist die nach dieser Methode gewonnene Lösung im Allgemeinen nur eine Näherung der exakten Lösung -b/a.
Beispiel für eine graphische Lösung einer linearen Gleichung mit einer Variablen
Wir betrachten die lineare Gleichung 3x + 15 = 10.
Durch Äquivalenzumformungen erhält man daraus die Gleichung 3x + 5 = 0.
Wir zeichnen die Funktion y = 3x + 5:
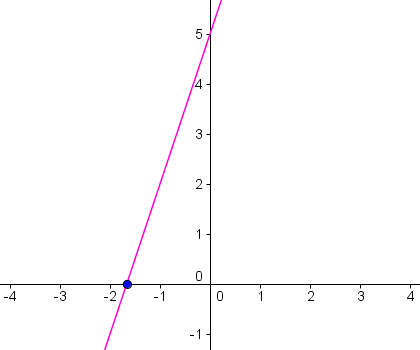
Als Nullstelle dieser Funktionen lesen wir xo = -1,7 ab. Dies ist eine Näherung für die exakte Lösung -5/3 = -1,666… .