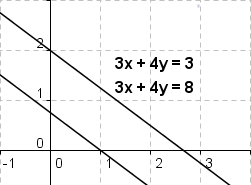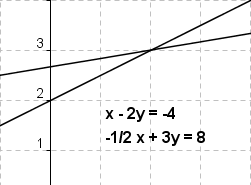Dieser Beitrag erklärt euch, wie man die Lösung eines linearen Gleichungssystems von zwei Gleichungen mit zwei Unbekannten graphisch bestimmen kann.
Lineares Gleichungssystem von zwei Gleichungen mit zwei Unbekannten
Ein lineares Gleichungssystem von zwei Gleichungen mit zwei Variablen (Unbekannten), z.B.
5x + 7y = 11
lässt sich graphisch lösen, indem man die Lösungen der beiden Gleichungen 2x + 3y = 4 und
5x + 7y = 11 (zwei Geraden) zusammen in demselben Koordinatensystem graphisch darstellt.
Dazu stellt man die beiden Gleichungen zunächst nach y um, d.h. man betrachtet sie einfach als lineare Funktionen y = mx + n:
2x + 3y = 4 | -2x
3y = -2x + 4 | :3
y = -2/3 x + 4/3
und
5x + 7y = 11 | -5x
7y = -5x + 11 | :7
y = -5/7 x + 11/7
Als nächstes werden die beiden Funktionen y = -2/3 x + 4/3 und y = -5/7 x + 11/7 in ein Koordinatensystem eingezeichnet und anschließend der Schnittpunkt (xs, ys) abgelesen:
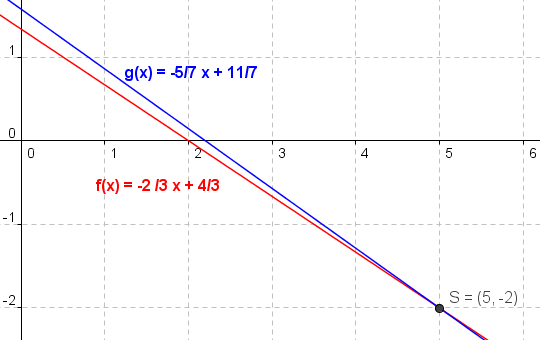
Der Schnittpunkt S hat in diesem Fall die Koordinaten (5, -2), d.h. (x, y) = (5, -2) ist einzige Lösung des gegebenen Gleichungssystems.
Drei verschiedene Fälle
In dem Beispiel von oben ergab sich ein Schnittpunkt der beiden Geraden, was gleichbedeutend damit ist, dass das vorgelegte Gleichungssystem genau eine Lösung besitzt.
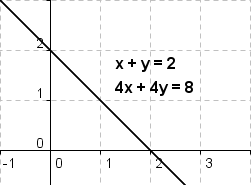
Nun weiss man aber von solchen Gleichungssystemen, dass sie auch keine bzw. unendlich viele Lösungen besitzen können. Beim Zeichnen der Geraden hätte man dann festgestellt, dass sie zueinander parallel liegen bzw. zusammenfallen.
Beim graphischen Lösen eines linearen Gleichungssystems von zwei Gleichungen mit zwei Unbekannten sind also die folgenden drei Fälle denkbar:
| Das Gleichungssystem hat keine Lösung. Die Geraden liegen (nicht zusammenfallend) parallel zueinander. |
 |
| Das Gleichungssystem hat unendlich viele Lösungen. Die Geraden fallen zusammen. |
 |
| Das Gleichungssystem hat genau eine Lösung. Die Geraden schneiden einander. |
 |