Lagebeziehung zwischen zwei Geraden im Raum

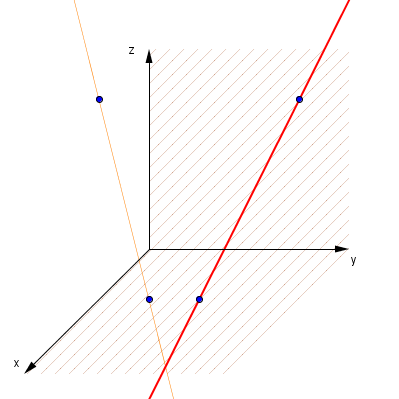
In diesem Beitrag geht es um die drei charakteristischen Lagebeziehungen zweier Geraden im Raum: parallel, ein gemeinsamer Schnittpunkt, windschief.

 

Zwei Geraden im Raum können zueinander auf drei unterschiedliche Art und Weisen liegen:
Sie können parallel sein (insbesondere identisch), sie können sich in genau einem Punkt schneiden oder sie können windschief sein, d.h. sie sind weder parallel noch haben sie einen Punkt gemeinsam.

 

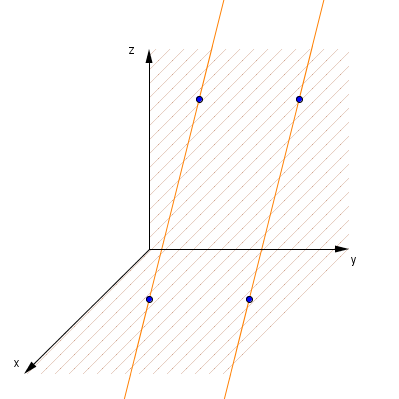
Parallele Geraden

Zwei Geraden im Raum sind parallel zueinander, wenn ihre Richtungsvektoren kollinear sind, d.h. wenn der Richtungsvektor der einen Geraden ein Vielfaches des Richtungsvektors der anderen Geraden ist und umgekehrt.

Hat z.B. eine Gerade den Richtungsvektor (1,2,3) und die andere Gerade den Richtungsvektor (3,6,9), so sind sie parallel, denn es ist

3 · (1,2,3) = (3,6,9)   bzw.   1/3 · (3,6,9) = (1,2,3).

Dagegen sind Geraden mit den Richtungsvektoren (1,2,3) und (2,4,5) nicht parallel, denn es lässt sich keine reelle Zahl s angeben, sodass

s · (1,2,3) = (2,4,5)   bzw.   1/s · (2,4,5) = (1,2,3)

wäre.

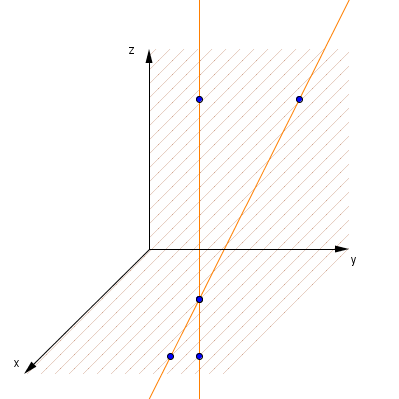
Ein gemeinsamer Schnittpunkt

Zwei nicht-parallele Geraden x = a + r·b und x = c + s·d haben genau dann einen gemeinsamen Schnittpunkt, wenn das Gleichungssystem

a + r·b = c + s·d

oder ausführlich

a_x + r·b_x = c_x + s·d_x
 
a_y + r·b_y = c_y + s·d_y
 
a_z + r·b_z = c_z + s·d_z

lösbar ist.

Windschiefe Geraden

Zwei nicht-parallele Geraden x = a + r·b und x = c + s·d liegen genau dann windschief zueinander, wenn das Gleichungssystem

a + r·b = c + s·d

nicht lösbar ist.

Auch interessant:

• Schema zur Untersuchung der Lagebeziehung zwischen zwei Geraden im Raum
• Lagebeziehung Geraden im Raum – Beispiel gemeinsamer Schnittpunkt
• Lagebeziehung Geraden im Raum – Beispiel windschiefe Geraden
• Lagebeziehung Geraden im Raum – Beispiel identische Geraden
• Lagebeziehung Geraden im Raum – Beispiel parallele Geraden