Was bedeuten die Begriffe Lineare Abhängigkeit und Lineare Unabhängigkeit einer Menge von Vektoren? In diesem Beitrag gibt es die Definitionen, Eigenschaften und Beispiele dazu.
Definition Lineare Unabhängigkeit
Eine Teilmenge M eines Vektorraums V heißt linear unabhängig, wenn
für jeden Vektor v ∈ M gilt: Lin ( M\{v} ) ≠ Lin M .
Das heißt also für jeden Vektor v ist der von M\{v} erzeugte Unterraum eine echte Teilmenge des von M erzeugten Unterraums.
Definition Lineare Abhängigkeit
Eine Teilmenge M eines Vektorraums V heißt linear abhängig, wenn sie nicht linear unabhängig ist.
Bei einer endlichen Menge von Vektoren {v1, … , vn} verzichtet man auch auf die Darstellung als Menge und spricht dann eben einfach von der linearen Abhängigkeit bzw. Unabhängigkeit der Vektoren v1, … , vn.
Beispiele
Die leere Menge ist nach Definition eine linear unabhängige Teilmenge eines jeden Vektorraums V.
Jede Teilmenge M eines Vektorraums V, die den Nullvektor enthält ist linear abhängig:
Es gilt dort nämlich Lin ( M\{0} ) = Lin M (der Nullvektor 0 kann die Bedingung aus der Definition für lineare Unabhängigkei nicht erfüllen).
{ (1,0) , (0,1) } ist ein linear unabhängiges Erzeugendensystem des IR2.
Dagegen ist { (1,0) , (0,1) , (3,4) } ein linear abhängiges Erzeugendensystem des IR2, denn man könnte jeweils einen der Vektoren (1,0) , (0,1) oder (3,4) entfernen und erhielte immer noch ein Erzeugendensystem für den IR2.
Folgerung
An den Definitionen und dem letzten Beispiel lässt sich folgendes erkennen:
Ist M eine Teilmenge eines Vektorraums V, dann gilt für jeden Vektor v aus V:
Aus v ∈ Lin M und v nicht in M folgt ( M U {v} ) ist linear abhängig.
0 als nicht-triviale Linearkombination von Vektoren
Ist V ein K-Vektorraum mit Nullvektor 0, dann nennt man 0 eine nicht-triviale Linearkombination von Vektoren v1, … , vn ∈ V, genau dann wenn es Skalare a1, … , an ∈ K gibt mit
a1·v1 + … + an·vn = 0 und mindestens ein ai ≠ 0.
Charakterisierung der Linearen Unabhängigkeit bzw. Abhängigkeit
Vektoren v1, … , vn eines Vektorraums V sind genau dann linear unabhängig, wenn der Nullvektor nur als triviale Linearkombination der Vektoren v1, … , vn darstellbar ist.
D.h. aus a1·v1 + … + an·vn = 0 folgt stets alle ai sind gleich Null.
Eine Teilmenge M eines Vektorraums V ist genau dann linear unabhängig, wenn entweder M die leere Menge ist oder wenn jede endliche Anzahl paarweise verschiedener Vektoren aus M linear unabhängig ist.
Eine Teilmenge M eines Vektorraums V ist genau dann linear abhängig, wenn es mindestens eine nicht-triviale Linearkombination des Nullvektors von paarweise verschiedenen Vektoren v1, … , vn aus M gibt.
Beispiel
Um also zu prüfen, ob z.B. die Vektoren (1,0,0), (0,3,4) und (-1,3,4) linear abhängig oder unabhängig sind, hat man einfach festzustellen ob es eine nicht-triviale Darstellung von 0 = (0,0,0) gibt oder nicht.
Dies ist gleichbedeutend mit der Untersuchung der Lösbarkeit des folgenden homogenen Gleichungssystems
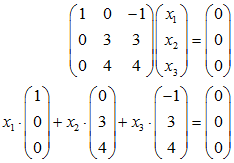
Fände man hier nur die triviale Lösung (x1,x2,x3) = (0,0,0), so hieße das, besagte Vektoren sind linear unabhängig. Tatsächlich sind diese Vektoren aber linear abhängig.