In diesem Beitrag wird euch an Beispielen erklärt, wie man die Lösungsmenge einer linearen Ungleichung mit zwei Variablen grafisch darstellen kann.
Sehen wir uns zunächst ein paar Beispiele für lineare Ungleichungen mit den beiden Unbekannten (Variablen) x und y an:
x + 2y – 3 > 0
-2x + 3y -4 < 0
3x + 4y > 5
-5y -21 < 7x
Jede dieser Ungleichungen lässt sich durch Äquivalenzumformungen entweder in die Form
oder aber in die Form
bringen.
Wir nehmen diese Umformungen für die Beispiele von oben vor und erhalten
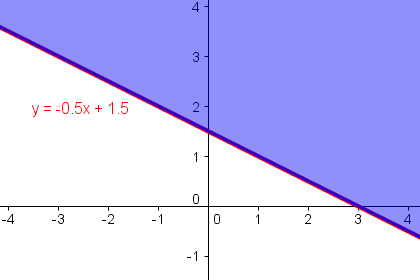
y > -x/2 + 3/2
y < 2/3 x + 4/3
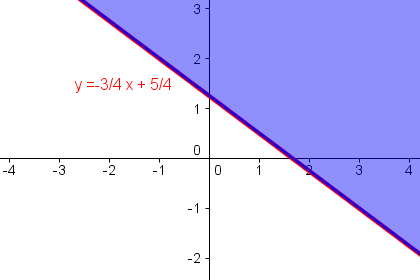
y > -3/4 x + 5/4
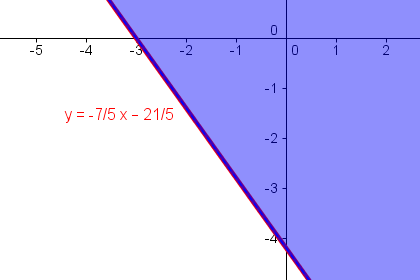
y > -7/5 x – 21/5
Die Lösungen einer solchen Ungleichung y < mx + n bzw. y > mx + n sind Punkte (x ; y) der Ebene, die sich grafisch folgendermaßen darstellen lassen:
Man zeichnet zuerst die Gerade y = mx + n.
Im Falle einer Ungleichung der Form y < … entspricht die Lösungsmenge der Halbebene unterhalb der Geraden.
Im Falle einer Ungleichung der Form y > … entspricht die Lösungsmenge der Halbebene oberhalb der Geraden.
Wir stellen nun die Lösungsmengen der Beispiele von oben grafisch dar:
Lösungsmenge von y > -x/2 + 3/2
Lösungsmenge von y < 2/3 x + 4/3

Lösungsmenge von y > -3/4 x + 5/4
Lösungsmenge von y > -7/5 x – 21/5