Mathe BLF Thüringen 2004 Pflichtaufgaben

Auf dieser Seite gibt es die original Pflichtaufgaben mit Lösungen der Mathe BLF Thüringen 2004 für euch.

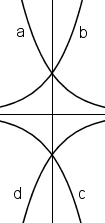
a)	Im Koordinatensystem rechts sind vier Funktionsgraphen abgebildet. Diese gehören zu den Funktionen f1(x)=2^x f2(x)=2^-x f3(x)=-2^x f4(x)=-2^-x Ordnen Sie die Graphen a,b,c,d der entsprechenden Funktion zu!
	Lösung einblendenLösung ausblenden
	Es ist b der Graph von f1(x)=2^x a der Graph von f2(x)=2^-x c der Graph von f3(x)=-2^x d der Graph von f4(x)=-2^-x.
*)	Paul Windig versucht die Aufgabe durch Raten zu lösen. Wie groß ist die Wahrscheinlichkeit, dass er alle vier Graphen richtig zuordnet?
	Lösung einblendenLösung ausblenden
	Die Anzahl der Möglichkeiten die Graphen a,b,c,d den Funktionen f1, f2, f3, f4 zuzuordnen, lässt sich so berechnen: Für Graph a gibt 4 mögliche Funktionen, nach Zuordnung von a gibt es für Graph b nur noch 3 mögliche Funktionen, nach Zuordnung von b gibt es für Graph c nur noch 2 mögliche Funktionen, nach Zuordnung von c gibt es für Graph d nur noch 1 mögliche Funktion. Das sind insgesamt 4! = 4·3·2·1 = 24 Möglichkeiten. Nur eine ist die richtige Zuordnung und damit beträgt die gesuchte Wahrscheinlichkeit p=1/24.
*)	Warum kann Paul niemals drei und nur drei richtige Zuordnungen treffen?
	Lösung einblendenLösung ausblenden
	Da jeder Graph zu genau einer Funktion gehört und umgekehrt jede Funktion zu genau einem Graphen, kann man nicht drei richtige Zuordnungen treffen und eine Falsche. Hat man drei richtige Zuordnungen gewählt, so gehört der letzte Graph definitiv zur letzten verbliebenen Funktion. Damit kann Paul entweder genau viermal richtig liegen oder aber weniger als dreimal.

b)	Zu jeder reellen Zahl a≠0 sei eine Funktion y = f_a(x) = a·sin x gegeben. Zeichnen Sie den Graph von f₃ im Intervall 0 ≤ x ≤ 2π!
	Lösung einblendenLösung ausblenden
	Der Graph von f₃(x) = 3·sin x ähnelt dem der Sinusfunktion. Anstelle von +1 haben nun die Hochpunkte von f₃ den y-Wert +3 und anstelle von -1 haben die Tiefpunkte von f₃ den y-Wert -3. Was die Periode und die Nullstellen angeht, so hat sich im Vergleich zur Sinusfunktion nichts geändert. Damit ergibt sich als Graph von f₃ das Bild unten.
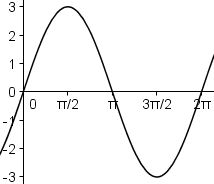
*)	Für a=1 hat die Tangente im Punkt P(π/3 \| ½√3) den Anstieg ½. Welchen Anstieg hat die Tangente im Punkt Q(2π/3 \| ½√3)?
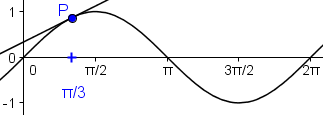
	Lösung einblendenLösung ausblenden
	Aus Symmetrie-Gründen ergibt sich ein Anstieg von -½.
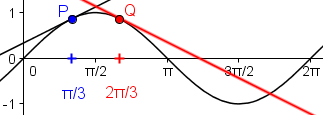
*)	Wenn f_a(1) = a·sin(1) = ½ gilt, welchen Wert hat dann f_a(π+1) = a·sin(π+1)?
	Lösung einblendenLösung ausblenden
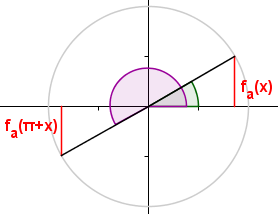
	Wegen -sin(α) = sin(180°+α) für 0° < α < 90° bzw. -sin(x) = sin(π+x) für 0 < x < π/2 bzw. -a·sin(x) = a·sin(π+x) für 0 < x < π/2 muss f_a(π+1) = -f_a(1) = -½ sein. Das Bild unten veranschaulicht den Sachverhalt.

c)	Die Funktion y = f(x) = ax³ geht durch den Punkt P(2 \| 10). Zu bestimmen ist a!
	Lösung einblendenLösung ausblenden
	Da f durch P(2 \| 10) verläuft, ist f(2) = 10. Also muss die Gleichung a·2³ = 10 nach a aufgelöst werden. Es ist 2³=8 und man erhält a·8 = 10 a = 10/8 = 1,25.
*)	Die Funktion y = g(x) = 2xⁿ geht durch den Punkt Q(√2 \| 16). Zu bestimmen ist n!
	Lösung einblendenLösung ausblenden
	Da g durch Q(√2 \| 16) verläuft, ist g(√2) = 16. Also muss die Gleichung 2·√2ⁿ = 16 nach n aufgelöst werden. Wegen √2ⁿ=2^n/2 und 2³=8 erhält man 2·2^n/2 = 16 2^n/2 = 8 n/2 = 3 n= 6.

d)	Berechnen bzw. vereinfachen Sie! log₃81, log_0,10,01, 1:(1/x^-1), √x⁸
	Lösung einblendenLösung ausblenden
	Der Taschenrechner liefert log₃81 = log 81/log 3 = 4. Man kann aber auch log₃81 = y umformen zu 3^y = 81 = 9·9=3·3·3·3. Also muss y = 4 sein. Der Taschenrechner liefert log_0,10,01 = log 0,01/log 0,1 = 2. Man kann aber auch log_0,10,01 = y umformen zu 0,1^y = 0,01 = 0,1·0,1. Also muss y = 2 sein. Es ist 1:(1/x^-1) = 1·(x^-1/1) = 1·x^-1 = x^-1. Es ist √x⁸ = x^8/2 = x⁴.

Auch interessant: