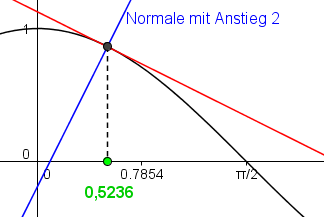
Gesucht ist in diesem Beispiel diejenige Stelle x, sodass die Funktion cos(x) dort eine Normale mit dem Anstieg 2 besitzt.
Aufgabe:
An welcher Stelle x mit 0 ≤ x ≤ π/2 besitzt die Cosinusfunktion eine Normale mit Anstieg 2?
Hinweise, Lösungsansatz:
Die Normale ist die Gerade, die senkrecht zur Tangente an den Graphen durch den Berührungspunkt geht.
Wenn die Tangente an dieser Stelle den Anstieg m hat, dann hat die Normale dort den Anstieg -1/m.
Damit lässt sich aus dem geforderten Anstieg 2 der Normale der Anstieg der Tangente berechnen.
Unter Verwendung der ersten Ableitung vom Cosinus kommt man dann auf die gesuchte Stelle x.
Lösung:
Die Normale an der gesuchten Stelle hat den Anstieg 2.
Damit hat die Tangente an der gesuchten Stelle den Anstieg -½.
Das gesucht x0 erfüllt also die Bedingung: cos'(x0) = -½.
Wegen cos'(x) = -sin(x) erhält man
-sin(x0) = -½ bzw. sin(x0) = ½.
Mit Hilfe vom Arkussinus findet man x0 = π/6 ≈ 0,5236.
Die Cosinusfunktion hat an der Stelle x0 = π/6 eine Normale mit dem
Anstieg 2.
Normale mit Anstieg 2 bei Cosinusfunktion