Auf dieser Seite findet ihr eine schnelle Einführung in die Prozentrechnung. Vollständig gelöste Übungsaufgaben (geeignet ab Klasse 6) sollen das Erklärte und die Formeln untermauern.
Das Prozent %
Für 1 % ist festgelegt: 1 % = 1 /100 = 0,01
oder mit anderen Zahlen:
5 % = 5 /100 = 0,05
10 % = 10/100 = 0,1
25 % = 25/100 = 0,25
50 % = 50/100 = 0,5
und ganz allgemein für irgendeine beliebige Zahl p:
Grundwert, Prozentwert, Prozentsatz
1 % von einer Größe G ist 1/100 · G = G/100
Beispiel: 1 % von 75 kg = 75 kg / 100 = 0,75 kg
p % von einer Größe G ist p/100 · G = p·G/100
Beispiel: 5 % von 500 Schülern = 5·500/100 Schüler = 25 Schüler
100 % entspricht dem Grundwert G
p % entspricht dem Prozentwert W
p heißt Prozentsatz
Dreisatz um Prozentwert W zu berechnen (G und p gegeben)
Von 25 Schülern der Klasse 7a haben 80 % Mathe als Lieblingsfach. Wieviele Schüler sind das?
| 100 % | → | 25 Schüler |
| 1 % | → | 25:100 Schüler |
| 80 % | → | 25:100·80 = 20 Schüler (G/100·p) |
Dreisatz um Grundwert G zu berechnen (W und p gegeben)
Nach 1,5 km sind 12 % einer Wanderstrecke zurückgelegt. Wie lang ist die Wanderstrecke insgesamt?
| 12 % | → | 1,5 km |
| 1 % | → | 1,5:12 km |
| 100 % | → | 1,5:12·100 = 12,5 km (W/p·100) |
Dreisatz um Prozentsatz p zu berechnen (W und G gegeben)
26 von 65 Gästen einer Hochzeitsparty gehören zur Familie des Bräutigams. Wieviel Prozent aller Gäste sind das?
| 65 Gäste | → | 100 % |
| 1 Gast | → | 100:65 % |
| 26 Gäste | → | 100:65·26 % = 40 % (100/G·W) |
Übersicht sämtlicher Berechnungs-Formeln
An den Dreisatzschemata kann man die Berechnungsformeln direkt ablesen. Wir geben sie hier in allen denkbaren Schreibweisen an:
| Prozentwert W berechnen: | |
| Grundwert G berechnen: | 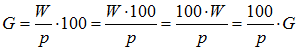 |
| Prozentsatz p berechnen: |
Verhältnisgleichung (Hosenträgerschema)
Jede der angegebenen Formeln lässt sich in die Verhältnisgleichung W/p = G/100 überführen.
Aus dieser Gleichung kann man sich das sogenannte Hosenträgerschema basteln
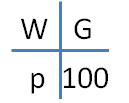
Mit diesem Schema lässt sich ebenfalls jede der drei Größen G, W oder p berechnen und zwar nach dem folgenden Muster:
Man trägt zunächst die beiden gegebenen Größen in das Hosenträgerschema ein.
Nun enthält das Schema 3 Zahlen und man rechnet die gesuchte Größe aus, indem man die sich diagonal gegenüberliegenden Zahlen multipliziert und mit der dritten Zahl dividiert:
3 Beispiele zum Hosenträgerschema
Von 240 Schülern eines Gymnasiums haben 80 % Mathe als Lieblingsfach. Wieviele Schüler sind das?
Mit dem Hosenträgerschema sieht das Ganze so aus:
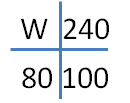
Man berechnet den gesuchten Prozentwert nun durch 80·240/100 und erhält W = 192 Schüler.
Nach 2,5 km sind 22 % eines Radweges zurückgelegt. Wie lang ist der Radweg insgesamt?
Das Hosenträgerschema sieht dann so aus:
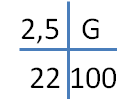
Man berechnet den gesuchten Grundwert nun durch 2,5·100/22 und erhält G = 11,36 km.
28 von 76 Gästen einer Silvesterparty kommen mit einem Taxi zur Party. Wieviel Prozent aller Gäste sind das?
Das zugehörige Hosenträgerschema sieht so aus:
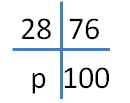
Man berechnet den gesuchten Prozentsatz nun durch 28·100/76 und erhält p = 36,84 %.
Clever mit Prozenten rechnen
Eine häufig vorkommende Aufgabe in der Prozentrechnung besteht darin, dass zu einer gegebenen Größe soundsoviel Prozent von dieser Größe hinzukommen bzw. abgezogen werden. Man fragt also nach G + p % von G bzw. G – p % von G.
Die beiden Berechnungsformeln lauten dann
G + p/100·G = G·(1 + p/100) bzw. G – p/100·G = G·(1 – p/100).
An den beiden folgenden Beispielen sieht man, wie einfach solche Aufgaben zu lösen sind:
Beispiel 1
Ein Fernseher für 999 Euro wird im Vorweihnachtsgeschäft um 15 % reduziert. Was kostet der reduzierte Fernseher?
Lösung: Der Preis des reduzierten Fernsehers entspricht 85 %. Wir rechnen also einfach
999 Euro · 0,85 und erhalten 849,15 Euro als neuen Preis.
Beispiel 2
In einem Online-Katalog für Werkzeug ist eine Bohrmaschine mit einem Nettopreis von 199 Euro angegeben. Was kostet die Bohrmaschine brutto, also einschließlich gesetzlicher Mehrwertsteuer in Höhe von 19 % ?
Lösung: Der Preis der Bohrmaschine mit Mehrwertsteuer entspricht 119 %. Wir rechnen einfach 199 Euro · 1,19 und erhalten 236,81 Euro als tatsächlichen Endpreis.
Darstellungsart wechseln
Zum Abschluss befassen wir uns noch damit, wie man aus Prozenten Brüche bzw. Kommazahlen macht und umgekehrt:
p % in einen Bruch umwandeln
→ schreibe p % als p/100 und kürze (erweitere) falls nötig – dies ergibt einen Bruch a/b
Beispiel: 6,4 % = 6,4/100 = 64/1000 = 8/125
p % in eine Kommazahl umwandeln
→ berechne p:100 (schriftlich oder mit Taschenrechner) – dies ergibt die Kommazahl
Beispiel: 42 % = 42:100 = 0,42
Bruch a/b in eine Kommazahl umwandeln
→ berechne a:b (schriftlich oder mit Taschenrechner) – dies ergibt die Kommazahl
Beispiel: 99/100 = 99:100 = 0,99
Bruch a/b in p % umwandeln
→ berechne a:b ·100 (schriftlich oder mit Taschenrechner) und häng % an – dies ergibt p %
Beispiel: 1/3 = 1:3 ·100 % = 33,33… % = 33 1/3 %
Kommazahl x in p % umwandeln
→ berechne x·100 (schriftlich oder mit Taschenrechner) und häng % an – dies ergibt p %
Beispiel: 0,021 = 0,021 ·100 % = 2,1 %
Kommazahl x in Bruch umwandeln
→ berechne y = x·10..0 (soviel Nullen wie x Nachkommastellen hat)
→ y/10..0 ist der Bruch, der sich evtl. noch kürzen lässt
Beispiel: 0,2345 = 0,2345·10000 / 10000 = 2345/10000 = 469/2000
Hinweis: Die letzte Methode funktioniert nur, falls x endlich viele Nachkommastellen hat.