Vektorrechnung – Aufgaben und Lösungen

Gegeben sind 4 Punkte A, B, C, D in einem kartesischen Koordinatensystem:

A( 2 | 2 | -2 )
B( 4 | -4 | 2 )
C( 8 | 2 | 2 )
D( 6 | 8 | -2 )

Aufgabe I

Zeige, dass das Dreieck ABC gleichschenklig ist!

Lösung:

Wir prüfen ob zwei Seiten des Dreiecks dieselbe Länge haben:

\vec{AB} = \begin{pmatrix} 4 - 2 \\ -4 - 2 \\ 2 - (-2) \end{pmatrix} = \begin{pmatrix} 2 \\ -6 \\ 4 \end{pmatrix} |\vec{AB}| = \sqrt{2^2 + (-6)^2 + 4^2} = \sqrt{4 + 36 + 16} = \sqrt{56} \vec{BC} = \begin{pmatrix} 8 - 4 \\ 2 - (-4) \\ 2 - 2 \end{pmatrix} = \begin{pmatrix} 4 \\ 6 \\ 0 \end{pmatrix} |\vec{BC}| = \sqrt{16 + 36 + 0} = \sqrt{52} \vec{CA} = \begin{pmatrix} 2-8 \\ 2-2 \\ -2-2 \end{pmatrix} = \begin{pmatrix} -6 \\ 0 \\ -4 \end{pmatrix} |\vec{CA}| = \sqrt{36 + 0 + 16} = \sqrt{52}

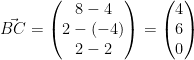
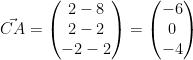
\vec{BC} und \vec{CA} haben die gleiche Länge, also ist das Dreieck ABC gleichschenklig.

Aufgabe II

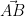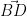Prüfe, ob \vec{AB} und \vec{BD} zueinander orthogonal sind!

Lösung:

\vec{AB} = \begin{pmatrix} 2 \\ -6 \\ 4 \end{pmatrix}  

\vec{BD} = \begin{pmatrix} 6-4 \\ 8-(-4) \\ -2-2 \end{pmatrix} = \begin{pmatrix} 2 \\ 12 \\ -4 \end{pmatrix}

Falls die beiden Vektoren orthogonal sind, müsste ihr Skalarprodukt Null sein:

\vec{AB} \cdot \vec{BD} = \begin{pmatrix} 2 \\ -6 \\ 4 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 12 \\ -4 \end{pmatrix} = 2 \cdot 2 + (-6) \cdot 12 + 4 \cdot (-4) = 4-72-16 \neq 0

\vec{AB} und \vec{BD} sind nicht orthogonal.

Aufgabe III

Die Diagonale 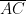\overline{AC} des Vierecks ABCD schneidet die x-y-Ebene im Punkt S(xS|yS|zS). Berechne die Koordinaten von S!

Lösung:

Die Diagonale 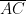\overline{AC} liegt auf der Geraden

\vec{x} = \vec{OA} + r \cdot \vec{AC} \vec{x} = \begin{pmatrix} 2 \\ 2 \\ -2 \end{pmatrix} + r \cdot \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix}

Der Punkt S liegt in der x-y-Ebene, also ist zS = 0 und S liegt auf der Geraden \vec{x} .

xS = 2 + r · 6
yS = 2 + r · 0
0 = -2 + r · 4

Die unterste Zeile liefert r = 1/2 , die mittlere Zeile yS = 2 und die oberste durch Einsetzen von 1/2 in r noch xS = 5.

Es ist S( 5 | 2 | 0 ).

Auch interessant: