Dieser Beitrag soll euch erklären, was Nullstellen von Funktionen sind. Es gibt Funktionen f(x), die für gewisse Werte x Null werden, zu den also ein oder mehrere Wertepaare der Form ( x, 0 ) gehören. Solche Wertepaare entsprechen Punkten auf der x-Achse.
Eine Zahl xo aus dem Definitionsbereich einer Funktion f heißt Nullstelle von f, wenn
f(xo) = 0 ist.
Die Nullstellen einer Funktion f sind diejenigen Stellen, an denen der Graph von f die x-Achse schneidet oder berührt.
Beispiel 1: Nullstelle von y = f(x) = 2x – 1
Für die Gleichung 0 = 2x – 1 erhält man als einzige Lösung x = ½, d.h. die einzige Nullstelle von f(x) = 2x – 1 befindet sich an der Stelle xo = ½.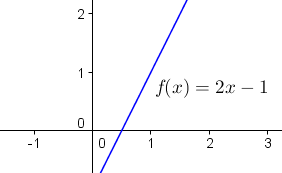
Beispiel 2: Nullstellen von y = f(x) = x2 – 4
Für die Gleichung 0 = x2 – 4 erhält man zwei Lösungen, nämlich x1 = -2 und x2 = 2. Dies sind die beiden Nullstellen von f(x) = x2 – 4.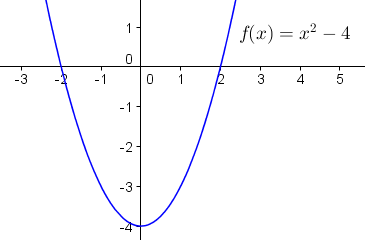
Beispiel 3: Unendlich viele Nullstellen von y = f(x) = sin(x)
Für die Gleichung 0 = sin(x) erhält man unendlich viele Lösungen xk, nämlich für jede ganze Zahl k die Lösung xk = k·π. Dies sind die unendlich vielen Nullstellen von f(x) = sin(x).