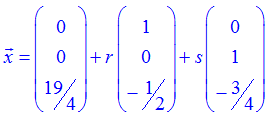Normalengleichung in Parametergleichung
Auf dieser Seite geht es darum, wie sich eine gegebene Normalengleichung einer Ebene in eine vektorielle Parametergleichung dieser Ebene umwandeln lässt.
Dazu sei die folgende Ebene E in Normalenform gegeben:
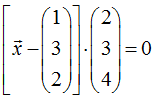
Eine Parametergleichung dieser Ebene lässt sich auf zwei verschieden Weisen herstellen. Für beide Varianten benötigt man zunächst die Koordinatenform der Ebene. Dazu bringen wir die gegebene Normalengleichung in die folgende Form
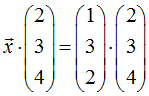
und schreiben Vektor →
x komponentenweise mit x, y, z
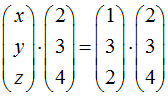
Ausrechnen des Skalarproduktes auf beiden Seiten liefert die Koordinatenform
Aus dieser Darstellung können wir nun problemlos eine Parametergleichung der Ebene gewinnen.
Variante I – Drei-Punkte-Gleichung
Wir setzen y = z = 0 und erhalten x = 19/2 = 9,5 und damit den Punkt
Wir setzen x = z = 0 und erhalten y = 19/3 und damit den Punkt
Wir setzen x = y = 0 und erhalten z = 19/4 und damit den dritten Punkt
Mit diesen drei Punkten A, B, C bilden wir nun die Parametergleichung der betrachteten Ebene und erhalten
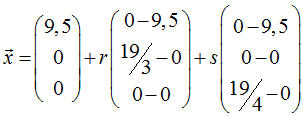
und schließlich die Gleichung
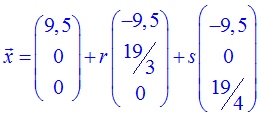
Variante II – Direkte Parametrisierung
Wir benutzen erneut die zuerst hergestellte Koordinatenform
Nun setzen wir
y := s
stellen die Koordinatenform nach z um und ersetzen darin x bzw. y durch r bzw. s:
4z = 19 – 2x – 3y
z = 19/4 – 1/2x – 3/4y
z = 19/4 – 1/2r – 3/4s
Somit haben wir drei Gleichungen für die drei Komponenten x, y, z des allgemeinen Vektors →
x
y = 0 + r · 0 + s · 1
z = 19/4 + r · (-1/2) + s · (-3/4)
also in Vektorschreibweise