In diesem Beitrag geht es um Geradenscharen. Zunächst wird erklärt, was eine Geradenschar ist und dann ein typisches Beispiel für die Bestimmung einer speziellen Geraden aus einer Geradenschar durchgerechnet.
Enthält die Gleichung einer Geraden
![]()
neben dem Geradenparameter r noch eine weitere Variable t, wie zum Beispiel in
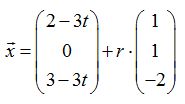
so spricht man von einer Geradenschar gt, da zu jedem Wert von t eine spezielle Gerade gt gehört.
Das folgende Bild zeigt drei Geraden zum Beispiel von oben für t = 0, t = 1 und t = 2:
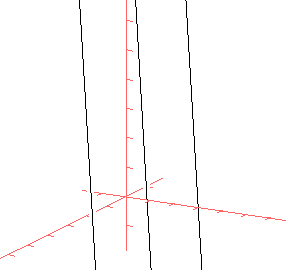
In den Anwendungen geht es in der Regel darum, aus der Geradenschar eine spezielle Gerade herauszufiltern, die eine ganz bestimmte Eigenschaft erfüllt. So kann man etwa danach fragen, welche Gerade aus der Schar
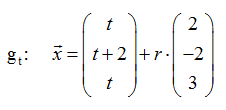
die z-Achse schneidet?
Die Gerade, die wir suchen, muss einen Punkt (0 ; 0 ; z) enthalten mit einer gewissen reellen Zahl z. Die x- und y-Koordinate dieses Punktes müssen Null sein, da er ja auf der z-Achse liegt.
Wir machen also den Ansatz
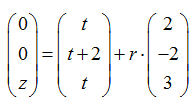
und erhalten somit das Gleichungssystem
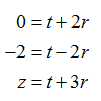
Dies führt auf t = -1 , r = 0,5 und z = 0,5. Die Gerade g-1 schneidet also die z-Achse im Punkt (0 ; 0 ; 0,5).