In diesem Beitrag wird erklärt, wie man Lösungspaare linearer Gleichungen bestimmen kann. Hier geht es also um lineare Gleichungen, die genau zwei Unbekannte x,y (oder zwei beliebige andere Buchstaben) enthalten.
Worum geht es?
Es geht darum zu einer Gleichung wie etwa
![]()
passende Zahlenpaare (x,y) zu finden, sodass mit diesen Zahlen die besagte Gleichung richtig, d.h. zu einer wahren Aussage wird. Dazu bieten sich zwei Möglichkeiten an.
Möglichkeit 1
Wir wählen willkürlich für x verschieden Werte aus, setzen diese in die Gleichung ein und berechnen damit das zugehörige y:
Setze x = 0
→ 3y + 0 = 3
→ 3y = 3
→ y = 3/3 = 1
→ Lösungspaar: (0 , 1)
Setze x = 2
→ 3y + 2 = 3
→ 3y = 1
→ y = 1/3
→ Lösungspaar: (2 , 1/3)
Wir können auch genauso gut y willkürlich festlegen:
Setze y = 0
→ 0 + x = 3
→ x = 3
→ Lösungspaar: (3 , 0)
Diese Methode führt man nun einfach so lange durch, bis man (je nach Aufgabenstellung) genügend Lösungspaare ermittelt hat.
Möglichkeit 2
Wir stellen die Gleichung nach einer Variablen um und erstellen eine Wertetabelle. Üblicherweise stellt man nach y um, weil man dann die Form y = mx + n erhält. In dieser Form werden normalerweise lineare Funktionen angegeben und nun wird klar, dass jede unserer Gleichungen mit zwei Unbekannten einer linearen Funktion und damit einer Geraden in der xy-Ebene entspricht.
Wir demonstrieren das Gesagte an der Gleichung von oben:
3y + x = 3 | -x
3y = 3 – x | :3
y = 1 – x/3
oder etwas angenehmer zu lesen als
y = -1/3 x + 1
Mit Hilfe des Anstiegs -1/3 und des y-Achsenabschnittes +1 könnte man die Gerade schon jetzt zeichnen. Jeder Punkt (x|y) auf der Geraden enstpricht dann einem Lösungspaar (x,y) unserer Ausgangsgleichung 3y + x = 3 bzw. einem Lösungspaar der umgeformten Gleichung y = -1/3 x + 1.
Wir wollen aber zunächst eine Wertetabelle angeben, da es uns ja um die Bestimmung von Lösungspaaren ging:
| x | 0 | 1 | 2 | 3 | … |
| y = -1/3 x + 1 | 1 | 2/3 | 1/3 | 0 | … |
Wir könnten theoretisch unendlich viele Lösungspaare angeben und haben hier mal eben
(0 , 1) , (1 , 2/3) , (2 , 1/3) , (3 , 0) ermittelt.
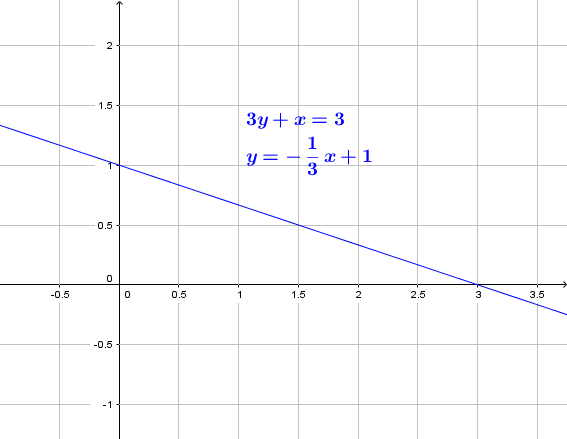
Lineare Gleichung anschaulich als Gerade
Ein weiteres Beispiel
4y – 8x = 8 mit Methode 1:
Setze x = 0
→ 4y – 0 = 8
→ 4y = 8
→ y = 8/4 = 2
→ Lösungspaar: (0 , 2)
Setze y = 0
→ 0 – 8x = 8
→ -8x = 8
→ x = -8/8 = -1
→ Lösungspaar: (-1 , 0)
und nun durch Umformung und Wertetabelle:
4y – 8x = 8 | +8x
4y = 8x + 8 | :4
y = 2x + 2
| x | -1 | 0 | 1 | 2 | … |
| y = 2x + 2 | 0 | 2 | 4 | 6 | … |
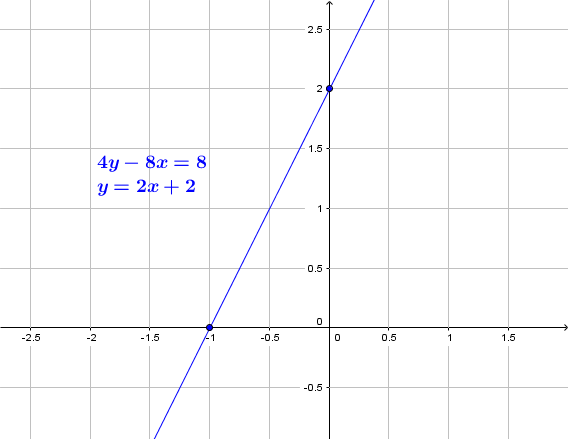
Man beachte, dass zum Zeichnen einer Geraden bereits zwei Punkte reichen. Mit Methode 1 kann man sich also schnell mal die Gleichung grafisch veranschaulichen.
Braucht man mehr als zwei Lösungspaare oder möchte man die Gerade mit einem grafikfähigen Taschenrechner darstellen, kann Methode 2 die bessere Wahl sein.