3 Aufgaben und Lösungen zu Exponentialfunktionen – es werden Wertetabellen erstellt, Graphen gezeichnet und es wird überprüft, ob gewisse Punkte zum Graph einer bestimmten Exponentialfunktion gehören können.
| x-Werte |
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
| y-Werte |
0,064
|
0,16
|
0,4
|
1
|
2,5
|
6,25
|
15,625
|
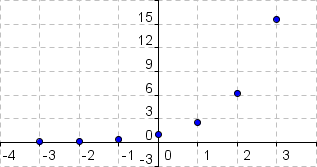Graph der Funktion:Wir verwenden zunächst die Wertetabelle, um die Punkte (x|y), die zur Funktion gehören, einzuzeichnen.
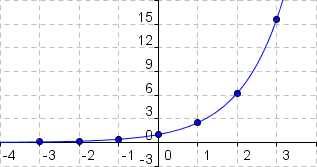Anschließend verbinden wir die eingezeichneten Punkte und erhalten so den gewünschten Graphen der Funktion.Erstelle für die Funktion f(x) = 0,3x eine Wertetabelle für -3 ≤ x ≤ 3 mit der Schrittweite 0,5. Zeichne den Graphen der Funktion in ein Koordinatensystem!
| x-Werte |
-3
|
-2,5
|
-2
|
-1,5
|
-1
|
-0,5
|
0
|
| y-Werte |
37,04
|
20,29
|
11,11
|
6,09
|
3,33
|
1,83
|
1
|
| x-Werte |
0,5
|
1
|
1,5
|
2
|
2,5
|
3
|
|
| y-Werte |
0,55
|
0,3
|
0,16
|
0,09
|
0,05
|
0,03
|
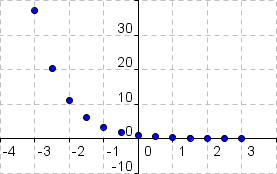Graph der Funktion:Wir verwenden zunächst die Wertetabelle, um die Punkte (x|y), die zur Funktion gehören, einzuzeichnen.
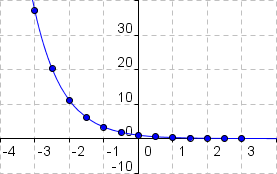Anschließend verbinden wir die eingezeichneten Punkte und erhalten so den gewünschten Graphen der Funktion.Stelle fest, ob die Punkte A(2|0,16) und B(-3,5|30) auf dem Graphen der Funktion f(x) = 0,4x liegen!
Falls A auf dem Graphen von f liegt, dann müsste f(2) = 0,16 gelten. Wir prüfen:
f(2) = 0,42 = 0,16. Damit liegt A auf dem Graphen von f.
Falls B auf dem Graphen von f liegt, dann müsste f(-3,5) = 30 gelten. Wir prüfen:
f(-3,5) = 0,4-3,5 = 24,705 ≠ 30. Damit liegt B nicht auf dem Graphen von f.