In diesem Beitrag geht es um Aufgaben zur Kurvendiskussion von Funktionen, in denen die e Funktion (Exponentialfunktion) involviert ist. Die erste Kurvendiskussion wird ausführlich vorgeführt, im Anschluss daran finden sich zwei weitere Aufgaben mit Lösungen und graphischen Darstellungen.
Aufgabe:
Durchzuführen ist eine Kurvendiskussion mit der Funktion
f(x) = x · e2-x,
d.h. Nullstellen, Extrempunkte, Wendepunkte, Verhalten im Unendlichen usw. sind zu bestimmen sowie der Graph der Funktion ist zu zeichnen.
Lösung:
Los geht es mit der Bestimmung des Schnittpunktes von f mit der y-Achse:
f(0) = 0 · e2-0 = 0
d.h. der Graph der Funktion geht durch den Punkt (0 ; 0).
Damit haben wir auch gleichzeitig die einzige Nullstelle von f ermittel:
x0 = 0.
Eine weitere Nullstelle kann es nicht geben, da das Produkt
x · e2-x
wegen e2-x > 0 genau dann Null wird, wenn x gleich Null ist.
Als nächstes suchen wir die Extrempunkte von f. An den Stellen wo f Extrempunkte hat, muss ihre erste Ableitung f´ gleich Null sein. Es ist
f(x) = x · e2-x = u(x) · v(x)
mit u(x) = x, u´(x) = 1 und v(x) = e2-x, v´(x) = -e2-x
und mit der Produktregel erhält man für die erste Ableitung
f´(x) = u´(x)·v(x) + u(x)·v´(x) = (1 – x) e2-x.
f´ wird genau dann Null, wenn der Faktor (1 – x) gleich Null ist. Damit liegt ein möglicher Extrempunkt bei der Stelle
xE = 1.
Mit Hilfe der zweiten Ableitung von f prüfen wir nun, ob
f´´(xE) ≠ 0
also ob tatsächlich ein Extrempunkt vorliegt und ob es sich um einen Hochpunkt (Maximum) oder um einen Tiefpunkt (Minimum) handelt.
Erneute Anwendung der Produktregel auf f´(x) = (1 – x) e2-x liefert die zweite Ableitung
f´´(x) = (x – 2) e2-x.
Wir erhalten
f´´(xE) = f´´(1) = (1 – 2) e2-1 = -e < 0,
was bedeutet, dass f an der Stelle xE = 1 ein lokales Maximum, also einen Hochpunkt HP besitzt.
Dieser Hochpunkt hat die Koordinaten HP = (1 ; f(1)) = (1 ; e).
Wir schauen nun noch nach möglichen Wendepunkten. Dazu müssen wir die zweite Ableitung f´´ auf Nullstellen untersuchen:
0 = f´´(x) = (x – 2) e2-x
führt auf die einzig mögliche Stelle xW = 2 für einen Wendepunkt (man beachte, dass obige rechte Seite der Gleichung nur Null wird, wenn der Faktor (x – 2) Null wird!).
Mit Hilfe der dritten Ableitung von f prüfen wir jetzt, ob es sich wirklich um eine Wendepunkt-Stelle handelt.
Nochmalige Anwendung der Produktregel liefert problemlos
f´´´(x) = (3 – x) e2-x.
Wir setzen xW = 2 in f´´´ ein und erhalten
f´´´(xW) = f´´´(2) = (3 – 2) e2-2 = 1 > 0.
Demnach gibt es einen Wendpunkt WP = (2 ; f(2)) = (2 ; 2) bei dem die Kurve von f von einer Rechtskrümmung zu einer Linkskrümmung überwechselt.
Drei charakteristische Merkmale des Graphen von f haben wir ermittelt: die Nullstelle, den Hochpunkt und den Wendepunkt.
Bevor man aber f zeichnen kann, muss man sich überlegen, was links und rechts von diesen markanten Stellen mit der Funktion passiert. Wir fragen also, wie sich die Funktionswerte entwickeln, wenn die Zahlen x beliebig groß bzw. beliebig klein werden, d.h. wir untersuchen das Verhalten im Unendlichen:
![]()
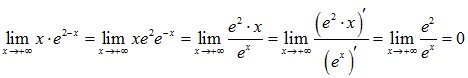
Bei der zweiten Grenzwertberechnung (für x gegen plus Unendlich) kommt übrigens die Regel von de L’Hospital zum Einsatz.
Damit haben wir schließlich alles zusammen, um den Graphen der Funktion
f(x) = x · e2-x zeichnen zu können:
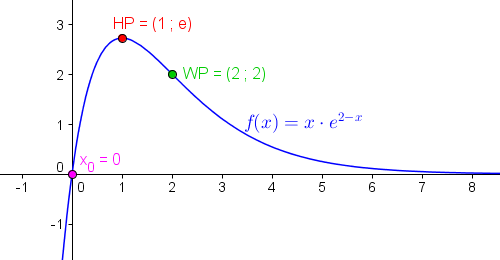
Graph der Funktion f(x) mit Nullstelle, Hochpunkt, Wendepunkt
Zwei weitere Aufgaben:
Da der Ablauf einer Kurvendiskussion bei allen Aufgaben mit e Funktion in etwa gleich verläuft, sind zu den beiden folgenden Aufgaben nur die Berechnungsergebnisse und die Graphen der Funktionen angegeben:
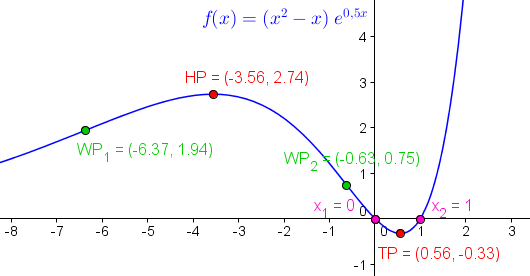
Kurvendiskussion von f(x) = (x2 – x) e0,5x
erste Ableitung: f´(x) = (1/2 x2 + 3/2 x – 1) e0,5x
zweite Ableitung: f´´(x) = (1/4 x2 + 7/4 x + 1) e0,5x
dritte Ableitung: f´´´(x) = (1/8 x2 + 11/8 x + 18/8) e0,5x
Schnittpkt. mit y-Achse: Sy = (0 ; 0)
Nullstellen: x1 = 0 , x2 = 1
Hochpunkt: HP = (-3,56 ; 2,74)
Tiefpunkt: TP = (0,56 ; -0,33)
Wendepunkte: WP1 = (-6,37 ; 1,94) , WP2 = (-0,63 ; 0,75)
Verhalten im Unendlichen: Limes für x gegen -∞ = 0, Limes für x gegen +∞ = +∞
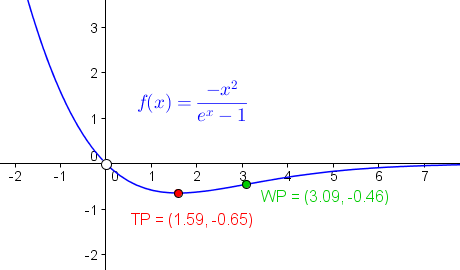
Kurvendiskussion von f(x) = -x2 / (ex – 1)
erste Ableitung: f´(x) = (ex(x-2) + 2) x / (ex – 1)2
zweite Ableitung:
f´´(x) = e2x (x2 – 4x + 2) / (ex – 1)3 + ex (x2 + 4x – 4) / (ex – 1)3 + 2 / (ex – 1)3
dritte Ableitung: f´´´(x) = h(x) / (ex – 1)4
mit h(x) = ex (x2 + 4ex(x2-3) + e2x(x2-6x+6) + 6x + 6)
Schnittpkt. mit y-Achse: existiert nicht, da f bei x = 0 nicht definiert ist
Nullstellen: keine, da der Zähler -x2 nur für x = 0 Null würde, die Funktion dort aber nicht definiert ist
Hochpunkte: keine
Tiefpunkt: TP = (1,59 ; -0,65)
Wendepunkt: WP = (3,09 ; -0,46)
Verhalten im Unendlichen: Limes für x gegen -∞ = +∞, Limes für x gegen +∞ = 0
Verhalten bei der Definitionslücke: Limes für x gegen 0 = 0