Eine Abbildung oder Funktion ist ein fundamentaler Begriff der Mathematik. Jede (mathematische) Abbildung beschreibt eine gewisse Zuordnung von Elementen einer Menge zu den Elementen einer weiteren Menge. Die genaue Festlegung des Begriffs lautet:
Existiert zu zwei Mengen A und B (die nicht leer sein dürfen) eine Zuordnung, die jedem Element aus der Menge A genau ein Element aus der Menge B zuordnet, so nennt man diese Zuordnung eine Abbildung von A in B.
Gibt man einer solchen Abbildung den Bezeichner f, so schreibt man in der Mathematik kurz und knapp
oder auch f(a)=b oder f: a→b, wenn dem Element a aus der Menge A das Element b aus der Menge B zugeordnet ist.
Beispiele
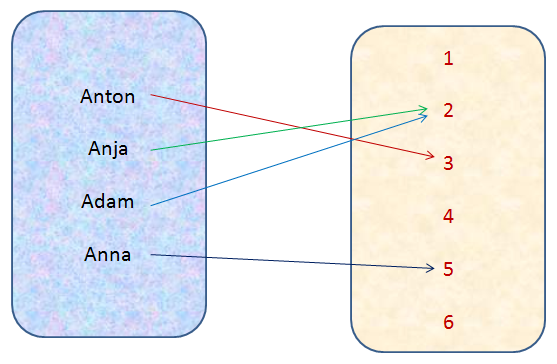
Die Abbildung f : S → M beschreibt die Zuordnung jedes Kindes der Familie Schmidt zu seiner aktuellen Mathenote.
Die Menge S enthält die Namen der vier Kinder Anton, Anja, Adam und Anne. M ist die Menge der möglichen Mathenoten, von denen allerdings nicht jede durch die Zuordnung auch in Anspruch genommen wird. Durch das abgebildete Pfeildiagramm ist eindeutig festgelegt, welche Mathenote zu welchem Kind gehört:
Eine weitere Abbildung g erhält man zum Beispiel, wenn man jedem Kind die Länge seines Namens zuordnet:
g(Anton) = 5
g(Anja) = 4
g(Adam) = 4
g(Anne) = 4
In der Schulmathematik sind die Abbildungen in der Regel Zuordnungen zwischen zwei Zahlenmengen: