Auf dieser Seite gibt es für euch den dritten Teil der original Analysis – Mathe Abituraufgaben mit Lösungen – aus Sachsen aus dem Jahre 1994.
Quelle der Aufgaben ist das Buch Abitur 2000, Stark Verlag, ISBN 3-89449-264-3.
Inhalt in Stichwörtern: gebrochenrationale Funktion, Definitionsbereich, Kurvendiskussion, Symmetrie, Nullstellen, Polstellen, Lücken, Extrempunkte (Hochpunkte und Tiefpunkte), Verhalten für x gegen ± Unendlich, Graph einer Funktion, Gleichung einer Tangenten
Aufgaben mit Lösungen – Teil 3
Wir betrachten die gebrochenrationale Funktion y = f(x) = ( x2 + 9 ) / ( 2x ).
Die erste Aufgabe besteht darin, den größtmöglichen Definitionsbereich der Funktion anzugeben!
Im Zähler x2 + 9 sind alle reelen Zahlen für x erlaubt. Der Nenner ist 2x. Der Term 2x könnte theoretisch auch alle reellen Zahlen vertragen. Allerdings darf ein Nenner nicht Null werden und man muss daher x = 0 ausschließen.
Somit ergibt sich als größtmöglicher Definitionsbereich IR ohne Null, also
IR\{0} = {x∈IR | x≠0}.
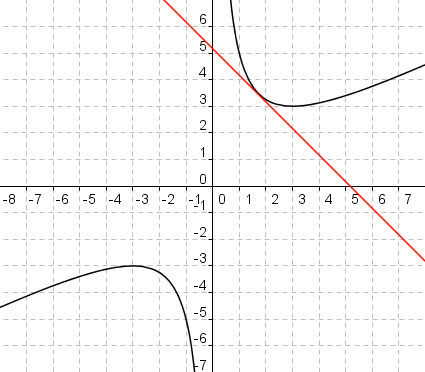
Die nächste Aufgabe besteht darin, eine vollständige Kurvendiskussion durchzuführen und den Graphen der Funktion f zu zeichnen!
Symmetrie:
Wie fragen uns zunächst, ob f achsensymmetrisch oder punktsymmetrisch ist? Dazu müssen die Bedingungen f(-x) = f(x) bzw. f(-x) = -f(x) geprüft werden:
f(-x) = ( (-x)2 + 9 ) / ( 2·(-x) )
= ( x2 + 9 ) / ( -2x )
= – ( x2 + 9 ) / ( 2x )
= – f(x)
Unsere Funktion f ist also symmetrisch zum Punkt (0|0).
Nullstellen:
Als nächstes wollen wir herausfinden, wo f den Wert Null annimmt. Dazu machen wir den Ansatz
0 = ( x2 + 9 ) / ( 2x ) .
Die rechte Seite wird genau dann Null, wenn der Zähler Null wird. Dies führt auf
0 = x2 + 9 .
Obige Gleichung hat keine reellen Lösungen und damit f keine Nullstellen.
Polstellen, Lücken:
Wir müssen uns zur Bestimmung von Polstellen und Lücken die Nullstellen des Nenners anschauen. Hier gibt es nur die Eine bei x = 0.
Eine Lücke läge nun vor, wenn 0 auch Nullstelle des Zählers wäre – was hier nicht der Fall ist. Es muss sich also bei x = 0 um eine Polstelle handeln. Die Frage ist nur, ob es sich um eine Polstelle mit oder ohne Vorzeichenwechsel handelt?!
Um das herauszufinden berechnen wir den linkseitigen und rechtsseitigen Grenzwert von f(x) für x gegen 0:
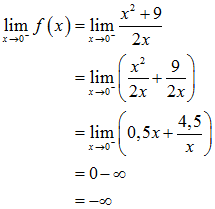
sowie
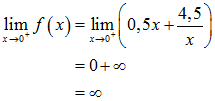
Die Funktion f hat somit bei x = 0 eine Polstelle mit Vorzeichenwechsel. Für x gegen Null von links strebt f(x) gegen minus Unendlich und für x gegen Null von rechts strebt f(x) gegen plus Unendlich.
Extrempunkte:
Als nächstes machen wir uns auf die Suche nach Hochpunkten und Tiefpunkten der Funktion. Dazu ermitteln wir die erste und zweite Ableitung von f.
Wir benutzen die Quotientenregel und erhalten für die erste Ableitung
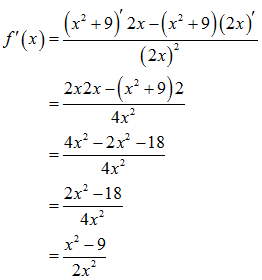
und für die zweite
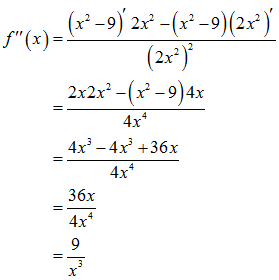
Mögliche Extremstellen sind die Nullstellen der ersten Ableitung:
0 = ( x2 – 9 ) / ( 2x2 )
bzw.
0 = x2 – 9 ,
woraus xE1 = 3 und xE2 = -3 folgt.
Ob es sich wirklich um Extremstellen handelt und falls ja, um was für welche, testen wir jetzt mit der zweiten Ableitung:
f´´(3) = 9/27 > 0 → lokales Minimum (Tiefpunkt) bei x = 3
f´´(-3) = 9/-27 < 0 → lokales Maximum (Hochpunkt) bei x = -3
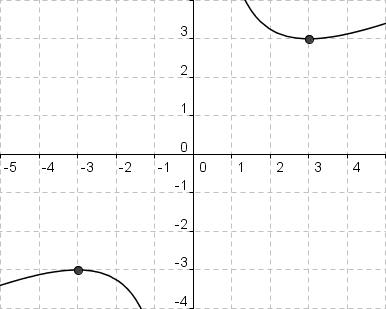
Damit gibt es zwei Extrempunkte: einen Hochpunkt bei ( -3 | f(-3) ) = ( -3 | -3 ) und einen Tiefpunkt bei ( 3 | f(3) ) = ( 3 | 3 ).
Verhalten für x gegen ± Unendlich:
Wie man an der Grenzwertberechnung oben schon gesehen hat, lässt sich f auch in der folgenden Form darstellen:
f(x) = x/2 + 9/(2x) ,
woran man sofort erkennt, dass für x gegen minus Unendlich f(x) gegen minus Unendlich strebt und für x gegen plus Unendlich f(x) auch gegen plus Unendlich strebt.
Graph der Funktion:
Inzwischen haben wir alle wichtigen Eigenschaften zusammengetragen und können die Funktion zeichnen. Wer noch etwas genauer zeichnen will, kann sich noch ein paar zusätzliche Punkte
( x | f(x) ) berechnen:
| x | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 |
| f(x) | -3,1 | -3 | -3,3 | -5 | 5 | 3,3 | 3 | 3,1 |
Eine weitere Aufgabe besteht jetzt darin, die Gleichung einer Tangenten an den Graphen von f anzugeben, die den gleichen Anstieg wie die Winkelhalbierende des zweiten und vierten Quadranten hat!
Die Winkelhalbierende des zweiten und vierten Quadranten ist die Gerade g(x) = -x. Sie hat den Anstieg m = -1. Wir müssen also zunächst herausfinden, wo unsere Funktion den Anstieg -1 hat und dann für den entsprechen Punkt besagte Tangente angeben.
Wir schauen jetzt also nach, für welche x die erste Ableitung von f den Wert -1 annimmt:
-1 = ( x2 – 9 ) / ( 2x2 ) | ·( 2x2 )
-2x2 = x2 – 9 | + 2x2
0 = 3x2 – 9 | + 9
3x2 = 9 | :9
x2 = 3
x1 = √3 , x2 = -√3
Wir entscheiden uns für die Stelle x = √3. Dort nimmt f den Funktionswert f(√3) = 3,464 an. Jetzt haben wir alles zusammen, um die Tangentengleichung aufzustellen:
yt = f´(xo)·(x – xo) + f(xo)
yt = -1·(x – √3) + 3,464
yt = -x + √3 + 3,464
yt = -x + 5,196 .