Bewegung eines Massenpunktes berechnen

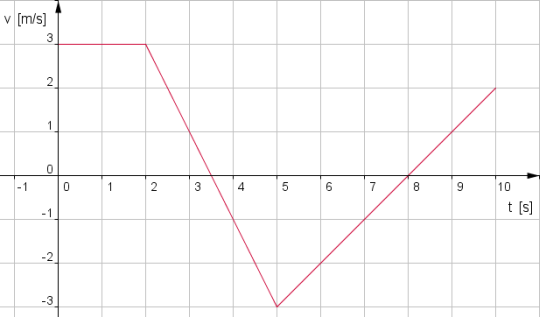
Ein Massenpunkt befindet sich zum Zeitpunkt t0 = 0 s im Ursprung Null der oben dargestellten Geraden und bewegt sich dann 10 s lang entsprechend dem unten abgebildeten t-v-Diagramm längs dieser Gerade.

Welchen Weg legt der Massenpunkt dabei insgesamt zurück und an welcher Stelle auf der Gerade befindet er sich bei t = 10 s ?

Wegen der Beziehung

1 s = \int v \; dt

ist der insgesamt zurückgelegte Weg

2 s_{gesamt} = \int\limits_{0}^{10} |v(t)| \; dt

Wir erhalten ihn also aus den drei Flächeninhalten A1, A2 und A3

A1
Trapez		 A_1 = \cfrac{3,5\;s + 2\;s}{2} \cdot 3 \; \cfrac{m}{s} = 8,25\;m
A2
Dreieck		 A_2 = \cfrac{1}{2} \cdot 4,5\;s \cdot 3 \; \cfrac{m}{s} = 6,75\;m
A3
Dreieck		 A_3 = \cfrac{1}{2} \cdot 2\;s \cdot 2 \; \cfrac{m}{s} = 2\;m

Der insgesamt zurückgelegte Weg beträgt

3 A_1 + A_2 + A_3 = 17\;m

Der Ort s(10 s), an dem sich der Massenpunkt nach 10 s befindet, ist die Flächenbilanz der drei Teilflächen A1, A2, A3. D.h. wir müssen A2 negativ zählen, da die Geschwindigkeit im Zeitintervall 3,5 s < t < 8 s negativ ist und erhalten somit

4 s(10\;s) = A_1 - A_2 + A_3 = 3,5\;m

Der Massenpunkt befindet sich nach 10 s rechts vom Punkt 0 und zwar an der Stelle 3,5 m.

Auch interessant: