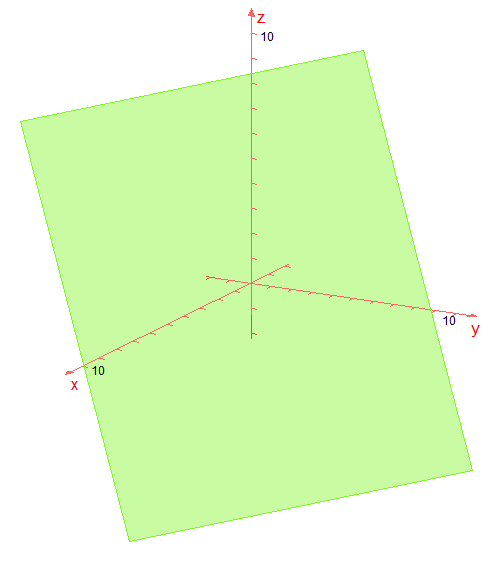
Koordinatengleichung in Parametergleichung
Auf dieser Seite geht es darum, wie sich eine gegebene Koordinatengleichung einer Ebene in eine vektorielle Parametergleichung dieser Ebene umwandeln lässt.
Zwei Möglichkeiten wollen wir uns hier ansehen und zwar die Methode über die Drei-Punkte-Gleichung und die Methode der Direkten Parametrisierung.
Gegeben sei also eine Ebene E in Koordinatenform:
Methode 1 – Drei-Punkte-Gleichung
Bei dieser Methode gewinnen wir zunächst aus der Koordinatenform drei Punkte A, B, C und bilden daraus eine Parametergleichung der Ebene.
Wir setzen x = y = 0 und erhalten z = -5/4 und damit A (0 ; 0 ; -5/4).
Wir setzen x = z = 0 und erhalten y = -5/3 und damit B (0 ; -5/3 ; 0).
Wir setzen y = z = 0 und erhalten x = -5/2 und damit C (-5/2 ; 0 ; 0).
Mit den drei Punkten lässt sich eine Parametergleich besagter Ebene problemlos aufbauen. Die Parametergleichung ausgedrückt mit den Punkten A, B und C lautet
![]()
bzw. mit den entsprechenden Zahlenwerten
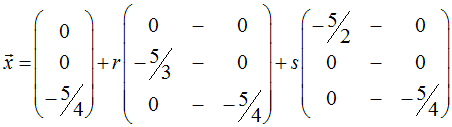
also schließlich
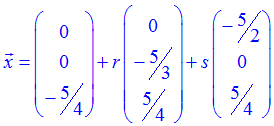
Kommen wir nun zu einer weiteren Methode, um die Koordinatengleichung 2x + 3y + 4z = -5 in eine Parametergleichung zu überführen.
Methode 2 – Direkte Parametrisierung
Wir setzen direkt x auf r und y auf s und stellen die Koordinatengleichung nach z um:
y = s
2r + 3s + 4z = -5
4z = -5 – 2r – 3s
z = -1,25 – 0,5r – 0,75s
Die drei Komponenten x, y, z des allgemeinen Vektors →
x lassen sich also so ausdrücken:
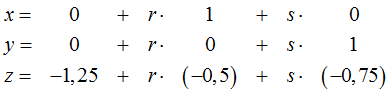
bzw. in Vektorschreibweise durch
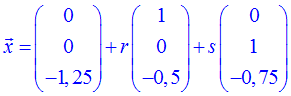
und wir sind fertig.