Koordinatengleichung und Achsenabschnittspunkte
In diesem Beitrag geht es um die Bestimmung der Achsenabschnittspunkte einer Ebene mit Hilfe einer Koordinatengleichung dieser Ebene.
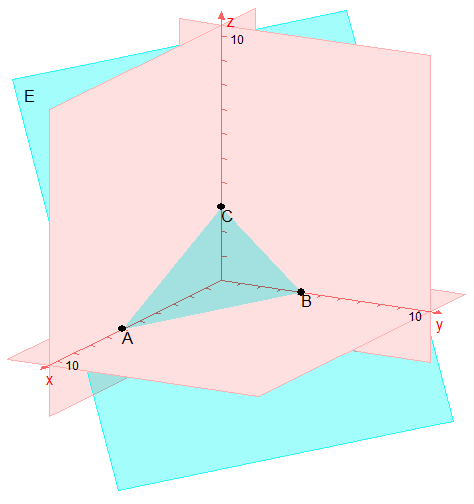
Als Achsenabschnittspunkte bezeichnet man die drei Punkte
in welchen die Koordinatenachsen die Ebene durchstoßen.
Eine Ebene ax + by + cz = d schneidet:
– die x-Achse im Punkt A (d/a ; 0 ; 0) , sofern a ≠ 0
– die y-Achse im Punkt B (0 ; d/b ; 0) , sofern b ≠ 0
– die z-Achse im Punkt C (0 ; 0 ; d/c) , sofern c ≠ 0
Sind die Koeffizienten a, b, c, d in der Koordinatengleichung alle ungleich Null, so lässt ax + by + cz = d umformen zu
Man bezeichnet dies als die Achsenabschnittsform der Ebene.
Nehmen wir als Beispiel die Ebene 2x + 3y +4z = 12. Wir berechnen der Reihe nach die drei Achsenabschnittspunkte A, B, C:
Setze y = z = 0. Dann ist 2x = 12, also x = 12/2 = 6.
Setze x = z = 0. Dann ist 3y = 12, also y = 12/3 = 4.
Setze x = y = 0. Dann ist 4z = 12, also z = 12/4 = 3.
Damit lautet die Achsenabschnittsform x/6 + y/4 + z/3 = 1 und die Achsenabschnittspunkte sind
A (6 ; 0 ; 0) B (0 ; 4 ; 0) C (0 ; 0 ; 3).
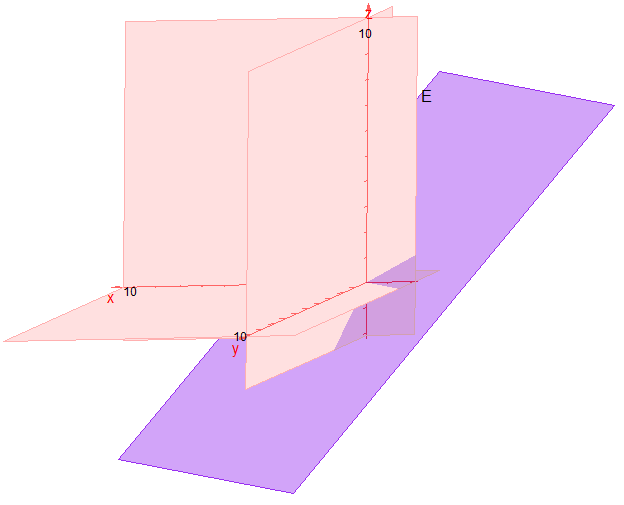
Existiert der Punkt A nicht, d.h. gibt es also keinen Schnittpunkt der Ebene mit der x-Achse, dann verläuft die Ebene parallel zur x-Achse. Dies ist genau dann der Fall, wenn in ax + by + cz = d der Koeffizient a Null ist, da sich in diesem Fall A (d/a ; 0 ; 0) nicht bilden lässt.
Dies gilt zum Beispiel für die Ebene 3y + 4z = 12
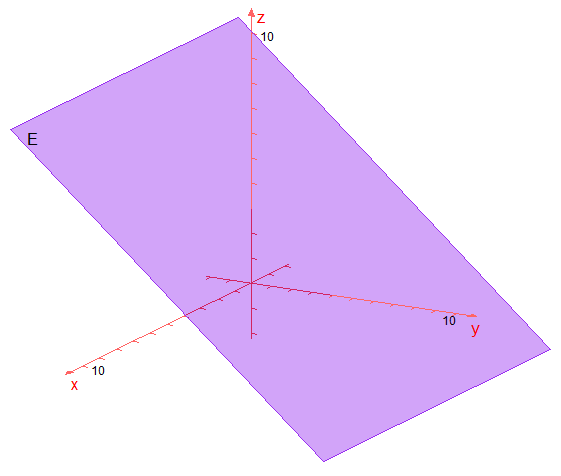
Entsprechende Aussagen gelten für den Fall, dass b = 0 bzw. c = 0 ist. Dann ist die Ebene parallel zur y-Achse bzw. zur z-Achse. So ist zum Beispiel ist 2x + 4z = 12 parallel zur y-Achse und 2x + 3y = 12 parallel zur z-Achse.
An den Punkten A (d/a ; 0 ; 0) , B (0 ; d/b ; 0) , C (0 ; 0 ; d/c) lässt sich noch etwas wichtiges ablesen:
Ist nämlich in der Koordinatengleichung ax + by + cz = d der Koeffizient d gleich Null, so gilt d/a = 0 und/oder d/b = 0 und/oder d/c = 0, sofern a und/oder b und/oder c von Null verschieden sind. Da stets mindestens einer der drei Koeffizienten a, b, c nicht Null ist, ist in diesem Fall stets einer der Punkte A, B, C gleich (0 ; 0 ; 0).
Das bedeutet die Ebene ax + by + cz = 0 geht durch den Ursprung. So zum Beispiel 2x + 3y + 4z = 0