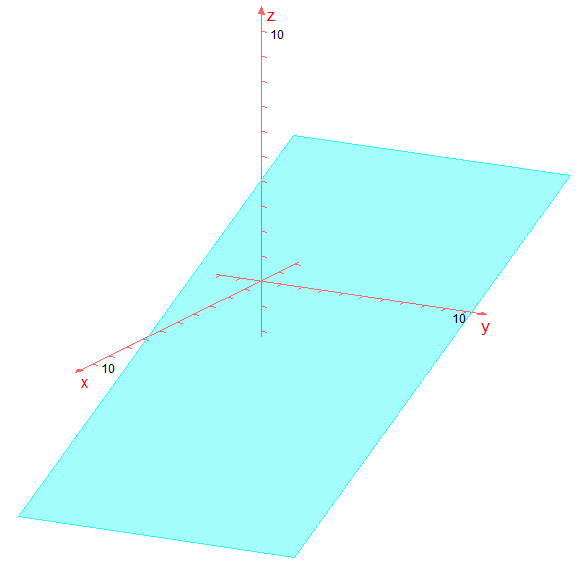
Parametergleichung in Koordinatengleichung
Auf dieser Seite geht es darum, wie sich eine gegebene vektorielle Parametergleichung einer Ebene in eine Koordinatengleichung dieser Ebene umwandeln lässt.
Dazu sei die folgende Ebene E in Parameterform gegeben:
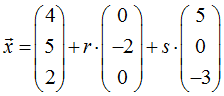
Wir schreiben den Vektor →
x ausführlich mit seinen Koordinaten x, y, z und erhalten zunächst
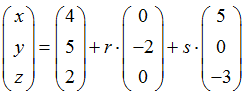
Damit haben wir folgendes System von drei Gleichungen vorliegen:
y = 5 – 2r
z = 2 – 3s
in der die Parameter r und s nicht mehr vorkommen!
Dazu befassen wir uns zunächst mit der ersten und der dritten Gleichung, um s zu eliminieren. Wir multiplizieren die erste Gleichung mit 3 und die dritte Gleichung mit 5 und erhalten:
5z = 10 – 15s
Addieren wir diese beiden neuen Gleichungen, so gibt das
Da der Parameter r nur in der Gleichung y = 5 – 2r vorhanden ist, sind wir an dieser Stelle schon fertig. Um das einzusehen gehen wir so vor:
Wir addieren die beiden verbliebenen Gleichungen
3x + 5z = 22
und erhalten
Um nun r ebenfalls zu eliminieren, ersetzen wir auf der rechten Seite der Gleichung den Ausdruck 5 – 2r durch y:
Für die Koordinatenform gehören allerdings alle Buchstaben auf eine Seite, d.h. wir rechnen nochmal minus y und erhalten die endgültige Form:
Aufgrund der fehlenden Variable y handelt es sich um eine Ebene parallel zur y-Achse.