Die Empirische Verteilungsfunktion F, auch Summenhäufigkeitsfunktion genannt, wird mit Hilfe der relativen Summenhäufigkeiten gebildet:
Seien x1 bis xk die ermittelten Merkmalsausprägungen sowie F1 bis Fk die zugehörigen relativen Summenhäufigkeiten.
Dann wird die Funktion F : IR –> [0 ; 1], definiert durch
F(x) = \begin{cases} 0 &, x
empirische Verteilungsfunktion genannt.
F(x) repräsentiert den Anteil an statistischen Einheiten, die einen Merkmalswert kleiner oder gleich x haben.
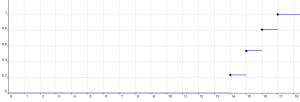
Aus dem Beispiel im Beitrag Relative Summenhäufigkeiten ergibt sich die folgende Empirische Verteilungsfunktion F (klick zum vergrößern):
Empirische Verteilungsfunktion F(x)