2 Aufgaben und Lösungen zu Exponentialfunktionen – es geht um die Bestimmung der Basen in den Exponentialfunktionen, wobei jeweils ein konkreter Punkt gegeben ist, durch den eine Funktion verlaufen soll.
Um die Gleichung f(x) = ax zu bestimmen, d.h. die Basis a konkret anzugeben, machen wir den Ansatz:
f(-3) = a-3 = 729
Die Gleichung a-3 = 729 müssen wir nun nach a auflösen:
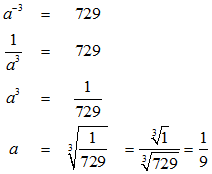
Somit lautet die gesuchte Exponentialfunktion f(x) = (1/9)x .
Gesucht ist die Gleichung einer Exponentialfunktion g(x) = bx, sodass der Punkt P(5|243) auf dem Graphen der Funktion liegt.
Um die Gleichung g(x) = bx zu bestimmen, d.h. die Basis b konkret anzugeben, machen wir den Ansatz:
g(5) = b5 = 243
Die Gleichung b5 = 243 müssen wir nun nach b auflösen:
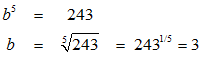
Somit lautet die gesuchte Exponentialfunktion g(x) = 3x .