Auf dieser Seite findet ihr Aufgaben mit Berechnungen am Kreiszylinder. Es geht hier darum, die Höhe von Zylindern zu berechnen, wobei der Radius und eine der drei Größen Oberfläche, Mantelfläche oder Volumen gegeben sind.
Höhe eines Zylinders berechnen
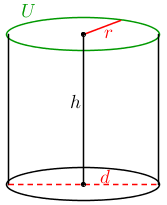
Aufgabe a)
geg: AM = 266,5 cm2 , r = 9 cm
ges: h
Lösung:
AM = 2 π r h
h = AM / (2 π r)
h = 266,5 cm2 / (2 π 9 cm)
h = 4,713 cm
Aufgabe b)
geg: AO = 444 cm2 , r = 4,5 cm
ges: h
Lösung:
AO = 2 π r (r + h)
AO / (2 π r) = r + h
AO / (2 π r) – r = h
h = AO / (2 π r) – r
h = 444 cm2 / (2 π 4,5 cm) – 4,5 cm
h = 11,203 cm
Aufgabe c)
geg: V = 138 cm3 , r = 1,5 cm
ges: h
Lösung:
V = π r2 h
h = V / (π r2)
h = 138 cm3 / (π (1,5 cm)2)
h = 19,523 cm