Auf dieser Seite geht es um die Lineare Hülle einer Menge von Vektoren und den Begriff des Erzeugendensystems. Neben den Definitionen werden Eigenschaften und Beispiele angegeben.
Lineare Hülle einer Menge von Vektoren
Sei M eine Teilmenge eines K-Vektorraums V. Dann wird durch die Linearkombinationen der Vektoren in M ein Unterraum von V aufgespannt oder erzeugt. Dieser Unterraum heißt Lineare Hülle von M und man schreibt dafür ⟨M⟩ oder Lin M. Man legt fest:
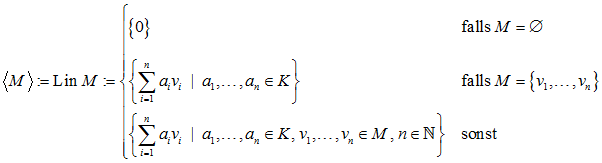
Erzeugendensystem
Ist V = ⟨M⟩, dann heißt M ein Erzeugendensystem von V.
Existiert ein endliches Erzeugendensystem von V, so sagt man V ist endlich erzeugbar oder endlich erzeugt.
Beispiel
Der IR2 besteht aus allen Vektoren der Form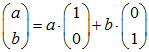 
, a,b ∈ IR.
Er ist also identisch mit der linearen Hülle der beiden Vektoren (1,0) und (0,1) und ist somit endlich erzeugbar.
Charakterisierung der Linearen Hülle
Ist M eine Teilmenge eines K-Vektorraums V, dann ist Lin M der kleinste Unterraum von V,
der M enthält. Es gilt also:
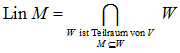
Weitere Eigenschaften der Linearen Hülle
Sind M und M‘ Teilmengen eines Vektorraums V, dann gilt:
- M ⊆ Lin M
- aus M ⊆ M‘ folgt Lin M ⊆ Lin M‘
- M = Lin M genau dann wenn M ist Unterraum von V
- Lin (Lin M) = Lin M
Spaltenraum einer Matrix – Lineare Hülle der Spalten einer Matrix
Man nennt den Unterraum, der aus allen Linearkombinationen der Spalten einer Matrix A gebildet wird, den Spaltenraum oder das Bild der Matrix A.
Ist A eine reelle m x n-Matrix
und bezeichnen die Vektoren v1, … , vn ∈ IRm die n Spalten der Matrix A,
dann ist der Spaltenraum von A die lineare Hülle ⟨v1, … , vn⟩ und ein Unterraum des IRm.
Ein lineares Gleichungssystem A x = b ist somit genau dann lösbar, wenn b zum Spaltenraum von A gehört.
Man erkennt dies sofort an der Darstellung A x = x1·v1 + … + xn·vn .