In diesem Beitrag geht es um stetige Funktionen. Zuerst wird der Begriff der Stetigkeit an einer Stelle angegeben und die wichtigsten stetigen Funktionen genannt. Anschließend wird an zwei Beispielen demonstriert, wie man auf Stetigkeit prüfen kann.
Eine einfache Möglichkeit Stetigkeit zu definieren lautet:
Eine Funktion heißt stetig an einer Stelle x0, wenn f(x0) existiert und mit dem Grenzwert der Funktionswerte f(x) für x gegen x0 übereinstimmt.
Die für die Schulmathematik wichtigsten Funktionen erweisen sich allesamt als stetig:
Polynomfunktionen, rationale Funktionen, die Betragsfunktion, Potenzfunktionen, Exponentialfunktionen, Logarithmusfunktionen sowie Sinus, Cosinus und Tangens sind stetig an jeder Stelle ihres entsprechenden Definitionsbereichs.
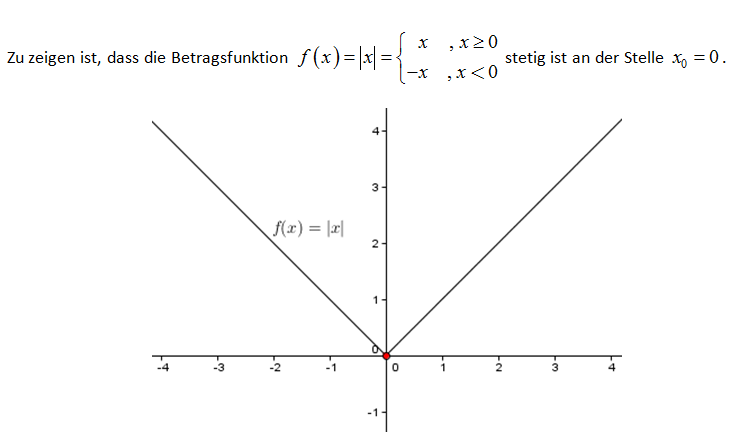
Die folgenden Beispiele demonstrieren, wie sich auf Stetigkeit prüfen lässt: