Auf dieser Seite findet ihr eine Übersicht wichtiger Eigenschaften von Sinus, Cosinus und Tangens.
Eigenschaften vom Sinus, y = sin x
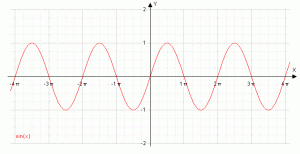
| Definitionsbereich | -∞ < x < ∞ |
| Wertebereich | -1 ≤ y ≤ 1 |
| monoton steigend | -π/2 + 2kπ ≤ x ≤ π/2 + 2kπ , k∈IZ |
| monoton fallend | 2kπ + π/2 ≤ x ≤ (2k+1)π + π/2 , k∈IZ |
| Nullstellen | xk = kπ , k∈IZ |
| Periode | 2π |
Eigenschaften vom Cosinus, y = cos x
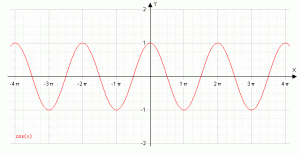
| Definitionsbereich | -∞ < x < ∞ |
| Wertebereich | -1 ≤ y ≤ 1 |
| monoton steigend | (2k-1)π ≤ x ≤ 2kπ , k∈IZ |
| monoton fallend | 2kπ ≤ x ≤ (2k+1)π , k∈IZ |
| Nullstellen | xk = (2k+1)·π/2 , k∈IZ |
| Periode | 2π |
Eigenschaften vom Tangens, y = tan x
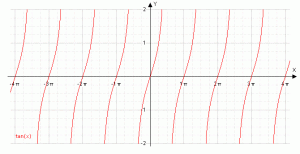
| Definitionsbereich | -∞ < x < ∞ x ≠ (2k+1)·π/2 , k∈IZ |
| Wertebereich | -∞ < y < ∞ |
| monoton steigend | kπ – π/2 < x < kπ + π/2 , k∈IZ |
| monoton fallend | nirgends |
| Nullstellen | xk = kπ , k∈IZ |
| Periode | π |