In diesem Beitrag geht es um Unterräume (lineare Teilräume) von Vektorräumen, die so genannten Untervektorräume.
Definition Untervektorraum
Eine Teilmenge U eines Vektorraums V heißt Untervektorraum von V (auch Unterraum oder linearer Teilraum), wenn U mit der Addition und skalaren Multiplikation von V selbst einen Vektorraum bildet.
Unterraum-Kriterium
Eine nichtleere Teilmenge U eines K-Vektrorraums V ist genau dann ein Unterraum von V, wenn folgendes gilt:
- v,w ∈ U → v + w ∈ U
- a ∈ K , v ∈ U → av ∈ U
Man sagt dann auch U ist abgeschlossen und der Addition und skalaren Multiplikation.
Die Bedingungen 1 und 2 im Unterraum-Kriterium lassen sich auch so ausdrücken:
Mit zwei Vektoren v und w enthält ein Unterraum auch jede Linearkombination av + bw dieser Vektoren.
Definition Linearkombination
Ist V ein K-Vektorraum, v1, … , vm ∈ V und a1, … , am ∈ K, dann heißt
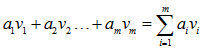
eine Linearkombination der Vektoren v1, … , vm.
Beispiele für Untervektorräume
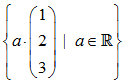ist ein Unterraum des IR3
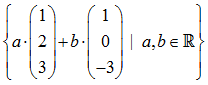ist ebenfalls ein Unterraum des IR3
Alle Geraden durch (0,0,0), alle Ebenen durch (0,0,0), der IR3 selbst und der Nullraum {(0,0,0)} sind alles Unterräume des IR3.
Lineare Hüllen sind Unterräume: Sind v1, … , vm Vektoren eines Vektorraums V, dann heißt die Menge aller Linearkombinationen dieser Vektoren die Lineare Hülle von v1, … , vm, in Zeichen ⟨v1, … , vm⟩. ⟨v1, … , vm⟩ ist ein Unterraum von V.
Die reellen 2×2-Diagonalmatrizen bilden einen Unterraum der reellen 2×2-Matrizen:
Addiert man zwei Diagonalmatrizen, dann erhält man wieder eine Diagonalmatrix und multipliziert man eine Diagonalmatrix mit einer reellen Zahl, so ergibt dies auch wieder eine Diagonalmatrix.
Durchschnitt und Summe von Unterräumen
Sind U und W Unterräume eines Vektorraums V, dann sind auch
Unterräume von V.