In diesem Beitrag geht es um Vektorräume. Was ist ein Vektorraum, welche Bedingungen müssen für das Vorhandensein eines Vektorraums erfüllt sein? Im Anschluss an die Definition gibt es die häufig verwendeten Standard-Beispiele für Vektorräume.
Definition Vektorraum
Ein Vektorraum V über einem Körper K (auch K-Vektorraum V) ist eine Menge V
mit einer Addition V x V → V
und einer skalaren Multiplikation K x V → V,
sodass für alle Vektoren u, v, w ∈ V und alle Skalare a, b ∈ K
die folgenden acht Bedingungen erfüllt sind:
- u + (v + w) = (u + v) + w
- v + w = w + v
- es gibt einen Nullvektor 0 mit v + 0 = v
- zu jedem Vektor v gibt es einen Vektor -v mit v + (-v) = 0
- (ab)v = a(bv)
- 1v = v
- a(v1 + v2) = av1 + av2
- (a + b)v = av + bv
Beispiele für Vektorräume
Kn sind Vektorräume: für jeden beliebigen Körper K bildet die Menge der n-Tupel
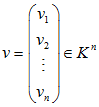
mit der komponentenweisen Addition und skalaren Multiplikation
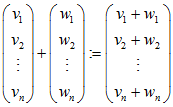
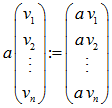
einen Vektorraum.
Insbesondere sind also die Ebene IR2 und der Anschauungsraum IR3 reelle Vektorräume.
Die Menge C0(I) aller auf einem Intervall I stetigen Funktionen bildet
mit der Addition (f + g)(x) := f(x) + g(x)
und der skalaren Multiplikation (a·f)(x) := a·f(x)
einen Vektorraum. Der Nullvektor ist hier die konstante Funktion f0: x→0.
Jeder Körper E mit einem Teilkörper K kann als ein K-Vektorraum aufgefasst werden.
Ist V irgend ein Vektorraum mit Nullvektor 0, dann ist der Nullraum { 0 } mit gleicher Addition und skalaren Multiplikation wie in V ebenfalls ein Vektorraum. Es handelt sich um den kleinstmöglichen Vektorraum überhaupt.
Ist V irgend ein Vektorraum und M eine nichtleere Menge, dann ist VM, die Menge aller Abbildungen von M nach V, wiederum ein Vektorraum.