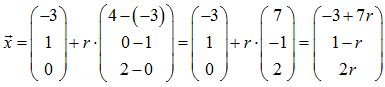Dieser Beitrag erklärt die vektorielle Zwei-Punkte-Gleichung einer Geraden. Mit Hilfe zweier Punkte A und B erhält man diese Darstellung einer Geraden im Raum.
Die vektorielle Zwei-Punkte-Gleichung einer Geraden g lautet
Vektor 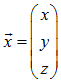 repräsentiert einen laufenden Punkt auf der Geraden, repräsentiert einen laufenden Punkt auf der Geraden, |
Vektor 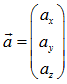 ist der Ortsvektor eines Punktes A, ist der Ortsvektor eines Punktes A, |
Vektor 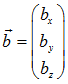 ist der Ortsvektor eines Punktes B, ist der Ortsvektor eines Punktes B, |
Das folgende Bild veranschaulicht diese Darstellungsart einer Geraden:
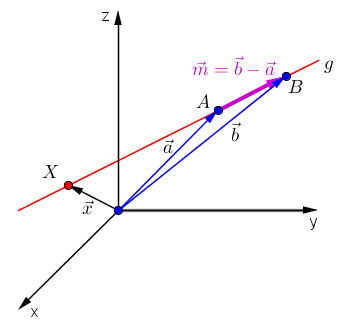
Vektorielle Zwei-Punkte-Gleichung einer Geraden
Beispiel:
Zu bestimmen ist die Gleichung einer Geraden g durch die Punkte
A = (1 ; 2 ; 3) und B = (3 ; 2 ; -1). Man erhält
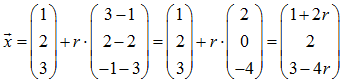
Beispiel:
Zu bestimmen ist die Gleichung einer Geraden g durch die Punkte
A = (-3 ; 1 ; 0) und B = (4 ; 0 ; 2). Man erhält