Auf dieser Seite gibt es für euch den vierten und letzten Teil der original Analysis – Mathe Abituraufgaben mit Lösungen – aus Sachsen aus dem Jahre 1994.
Quelle der Aufgaben ist das Buch Abitur 2000, Stark Verlag, ISBN 3-89449-264-3.
Inhalt in Stichwörtern: gebrochenrationale Funktion, Umfang eines Rechtecks, Minimum bestimmen, Fläche zwischen zwei Graphen, Schnittpunkt zweier Funktionen, bestimmtes Integral, Stammfunktion, quadratische Gleichung, pq Formel
Aufgaben mit Lösungen – Teil 4
In den folgenden Aufgaben geht es wieder um die gebrochenrationale Funktion
y = f(x) = ( x2 + 9 ) / ( 2x ).
Wir sollen ein x>0 so bestimmen, dass das Rechteck im Bild unten – repräsentiert durch die vier rosa Punkte – einen minimalen Umfang bekommt!
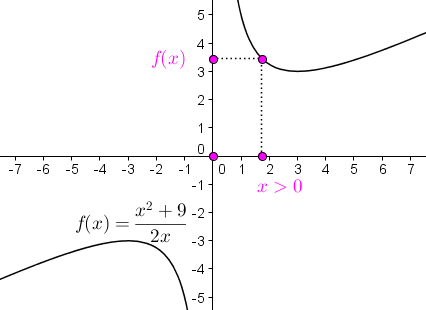
Der Umfang des Rechtecks ist x + f(x) + x + f(x), also:
2x + 2f(x)
= 2x + 2( x2 + 9 ) / ( 2x )
= 2x + ( x2 + 9 ) / x
= 2x + x + 9/x
= 3x + 9/x .
Wir fassen den Umfang als Funktion von x > 0 auf
U(x) = 3x + 9/x ,
deren Minimum wir zu ermitteln haben. Es ist
U´(x) = (3x)´ + (9/x)´ = 3 – 9/x2 .
Jetzt brauchen wir die Nullstellen dieser ersten Ableitung von U:
0 = 3 – 9/x2
-3 = -9/x2
-3x2 = -9
x2 = 3
xE1 = √3 und xE2 = -√3 .
xE2 können wir getrost vergessen, weil es der Bedingung x > 0 widerspricht. Wir testen also, ob bei xE1 = √3 ein Minimum vorliegt und benutzen dazu die zweite Ableitung von U:
U´´(x) = (3)´ – (9/x2)´ = 18/x3
U´´(√3) = 18/√33 > 0 → Minimum bei √3 .
Damit wird für x = √3 der Umfang des Rechtecks minimal (er ist U(√3) = 10,39).
In der nächsten Aufgabe ist die Fläche zwischen dem Graphen der Funktion f und zwischen dem Graphen der Geraden h1 = x/2 + 3 zu berechnen – und zwar über dem Intevall 1 ≤ x ≤ xs, wobei xs die x-Koordinate des Schnittpunktes von f und h1 bezeichnet!
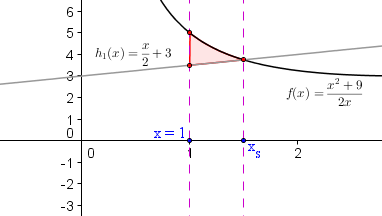
Wir berechnen die gesuchte Fläche natürlich mit Hilfe eines bestimmten Integrals, Dazu brauchen wir aber erst noch die Schnittstelle xs:
f(xs) = h1(xs)
(xs2 + 9)/(2xs) = xs/2 + 3
xs2 + 9 = xs2 + 6xs
9 = 6xs
xs = 1,5
Der Flächeninhalt ergibt sich nun aus der Berechnung des bestimmten Integrals von
f(x) minus h1(x) (eine passende Stammfunktion zu 9/(2x) – 3, s. unten, findet man schnell in jedem Tafelwerk). Man erhält schließlich A = 0,3246:
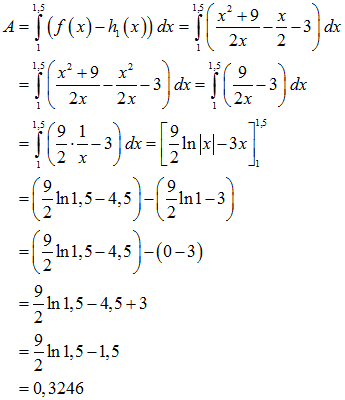
Als nächstes sollen wir ein a > 1 bestimmen, sodass die Fläche zwischen dem Graphen von f und der Geraden h2(x) = x/2 über dem Intervall 1 ≤ x ≤ a den Wert 2,25 annimmt!
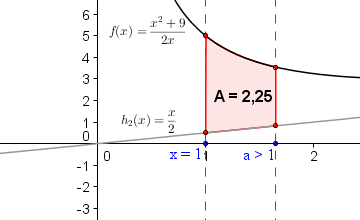
Auch diese Aufgabe lässt sich mit einem bestimmten Integral lösen, wobei wir jetzt die obere Integrationsgrenze a nicht kennen, aber dafür das Ergebnis 2,25:
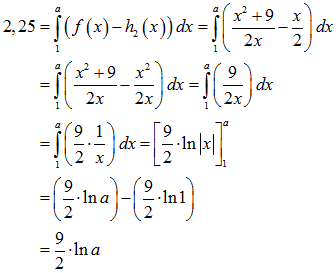
Wir lösen also noch die Gleichung 2,25 = 9/2 ln a:
2,25 = 9/2 ln a
4,5 = 9 ln a
0,5 = ln a
e0,5 = a
Das gesuchte a lautet somit a = e0,5 = 1.6487.
Für die letzte Aufgabe sind die Geraden g(x) = k mit k∈IR zu betrachten. Inwiefern hängt die Anzahl der Schnittpunkte des Graphen von f mit diesen Geraden von der Zahl k ab?
Die x-Koordinaten der Schnittpunkte bestimmt man bekanntlich mit dem Ansatz
f(x) = g(x)
hier also
(x2 + 9)/(2x) = k .
Das ist eine quadratische Gleichung, die keine, eine oder zwei Lösungen haben kann – was bedeutet es gibt keine, einen oder zwei Schnittpunkte. Indem wir diese quadratische Gleichung in Normalform x2 + px + q = 0 bringen und dann dazu die pq-Formel aufschreiben, erkennen wir den Einfluss des Parameters k:
(x2 + 9)/(2x) = k
x2 + 9 = 2kx
x2 – 2kx + 9 = 0
x1,2 = -p/2 ± √( p2/4 – q )
x1,2 = k ± √( k2 – 9 )
Es ergeben sich folgende Abhängigkeiten von k:
Ist k2 – 9 < 0, also
k2 < 9 bzw. k < 3 und k > -3 bzw. -3 < k < 3 ,
dann gibt es keine Lösungen x1, x2, also genau 0 Schnittpunkte.
Ist k2 – 9 = 0, also
k2 = 9 bzw. k = 3 oder k = -3 ,
dann gibt es eine Lösung x1 = x2, also genau 1 Schnittpunkt.
Ist k2 – 9 > 0, also
k2 > 9 bzw. k > 3 oder k < -3 ,
dann gibt es zwei verschiedene Lösungen x1 ≠ x2, also genau 2 Schnittpunkte.