Hier wird die Produktregel der Differentialrechnung hergeleitet. Zwei Beispiele zeigen, wie man damit die Ableitung einer Funktion bilden kann.
Die Produktregel
Sind die Funktionen f und g an einer Stelle x0 differenzierbar, dann ist auch die Funktion h = f · g an der Stelle x0 differenzierbar und es ist
h'(x0) = f'(x0) g(x) + f(x0) g'(x0)
Kurzform der Produktregel
Für (differenzierbare) f und g gilt
(fg)‘ = f‘ g + f g‘
Herleitung/Beweis der Produktregel
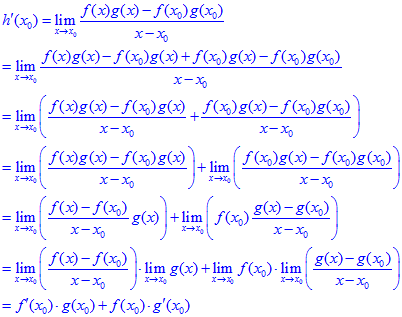
Beispiele
| f(x) | = (x2 + 2) · (x3 – 6) |
| f'(x) | = (x2 + 2)‘ · (x3 – 6) + (x2 + 2) · (x3 – 6)‘ = 2x · (x3 – 6) + (x2 + 2) · 3x2 = 2x4 – 12x + 3x4 + 6x2 = 5x4 + 6x2 – 12x |
| f(x) | = 1/x · √x , x>0 |
| f'(x) | = (1/x)‘ · √x + 1/x · (√x)‘ = -x-2 · √x + x-1 · 1/(2√x) = -2/(2x √x) + 1/(2x √x) = -1/(2x √x) |