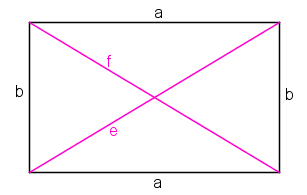
Ein Rechteck ist ein Viereck, in dem alle Innenwinkel gleich groß (nämlich 90°) sowie gegenüberliegende Seiten parallel und gleich lang sind.
Die Diagonalen e und f sind gleich lang und halbieren einander.
Der Umfang eines Rechtecks ist
U = 2(a + b) = 2a + 2b
Beispiele:
Gegeben ist ein Rechteck mit den Seiten a=12cm und b=8cm.
Gesucht ist der Umfang des Rechtecks.
Das Rechteck hat einen Umfang U = 2(12cm + 8cm) = 2·20cm = 40cm.
Gegeben ist der Umfang eines Rechtecks mit U=36cm sowie eine Seitenlänge a=10cm. Gesucht ist die Länge der anderen Seite b des Rechtecks.
Aus U = 2a + 2b erhält man 36cm = 20cm + 2b und daraus
2b = 36cm – 20cm = 16cm. Damit beträgt die Länge b = 16cm : 2 = 8cm.
Die Fläche (den Flächeninhalt) eines Rechtecks berechnet man durch
A = ab
Beispiele:
Gegeben ist ein Rechteck mit den Seiten a=12cm und b=8cm.
Gesucht ist der Flächeninhalt des Rechtecks.
Das Rechteck hat eine Fläche A = 12cm·8cm = 96cm2.
Gegeben ist die Fläche eines Rechtecks mit A=36cm2 sowie eine Seitenlänge b=9cm. Gesucht ist die Länge der anderen Seite a des Rechtecks.
Aus A = ab erhält man 36cm2 = a·9cm und daraus
a = 36cm2 : 9cm = 36:9 cm. Damit ist Seite a = 4cm.
Die Diagonalen e und f des Rechtecks berechnet man mit der Formel
e = f = Wurzel aus (a2 + b2)
Beispiel:
Gegeben ist ein Rechteck mit den Seiten a=4cm und b=3cm.
Gesucht sind die Diagonalen e,f.
Es ist e = Wurzel aus (a2 + b2) = Wurzel aus ((4cm)2 + (3cm)2), also
e = Wurzel aus (16cm2 + 9cm2) = Wurzel aus 25cm2.
Damit ist e = f = 5cm.