Auf dieser Seite gibt es für euch den ersten Teil der original Analysis – Mathe Abituraufgaben mit Lösungen – aus Sachsen aus dem Jahre 1994.
Quelle der Aufgaben ist das Buch Abitur 2000, Stark Verlag, ISBN 3-89449-264-3.
Inhalt in Stichwörtern: Natürlicher Logarithmus, Definitionsbereich, Funktionswerte, e-Funktion, Nullstellen, Graph, Gleichung einer Tangente, Gleichung eines Kreises, Schnittpunkt
Aufgaben mit Lösungen – Teil 1
Wir betrachten die Funktion y = f(x) = ln(2x – 1).
Als erstes soll der größtmögliche Definitionsbereich von f angegeben werden!
Mit ln ist der Natürliche Logarithmus gemeint, also die Logarithmusfunktion logex mit der Basis e=2,718… (Eulersche Zahl). Überhaupt alle Logarithmusfunktionen vertragen nur Argumente, die größer sind als Null. Für unsere Funktion f heißt das, es muss 2x – 1 > 0 sein.
Wir formen 2x – 1 > 0 um:
2x – 1 > 0 | +1
2x > 1 | :2
x > 0,5
Der größtmögliche Definitionsbereich von f ist damit die Menge {x aus IR | x > 0,5}.
Als nächstes sollen die Funktionswerte f(0,6), f(2,0) und f(5,0) berechnet werden!
Diese Aufgabe lösen wir natürlich mit einem Taschenrechner:
2·0,6 – 1 = 0,2 → ln(0,2) = -1,6
2·2,0 – 1 = 3,0 → ln(3,0) = 1,1
2·5,0 – 1 = 9,0 → ln(9,0) = 2,2
Sollte die Funktion ln nicht auf dem Taschenrechner hinterlegt sein, muss man an Stelle von ln(x) im Taschenrechner log(x):log(e) eingeben, wobei log die am Taschenrechner abgespeicherte Logarithmusfunktion und e die Eulersche Zahl ist.
Aus den Funktionswerten f(x)=0,5 und f(x)=1,5 ist nun das zugehörige Argument x zu ermitteln!
Für diese Aufgabe benötigt man die e-Funktion, also die Umkehrfunktion vom Natürlichen Logarithmus:
ln(2x-1) = 0,5 → 2x-1 = e0,5 → 2x = e0,5+1 → x = (e0,5+1)/2 = 1,3
ln(2x-1) = 1,5 → 2x-1 = e1,5 → 2x = e1,5+1 → x = (e1,5+1)/2 = 2,7
Zu bestimmen sind nun die Nullstellen von f !
Da jede Logarithmusfunktion logax bei x=1 ihre einzige Nullstelle besitzt, müssen wir uns fragen, wann 2x-1 denn Wert 1 annimmt. Wir lösen also die Gleichung 2x-1 = 1:
2x-1 = 1 | +1
2x = 2 | :2
x = 1
Die einzige Nullstelle von f(x) = ln(2x-1) liegt bei x=1.
Als nächstes soll der Graph von f im Intervall 0,6 ≤ x ≤ 5,0 dargestellt werden!
Um den Graphen in dem angegebenen Bereich zu zeichnen, verwenden wir die Wertepaare aus den oberen Aufgaben:
(0,6 , -1,6) , (1,3 , 0,5) , (2,0 , 1,1) sowie (2,7 , 1,5) , (5,0 , 2,2).
Wir legen ein Koordinatensystem an, tragen die Wertepaare als Punkte ein und verbinden diese. Dieses Vorgehen sollte in etwa folgendes Bild ergeben:
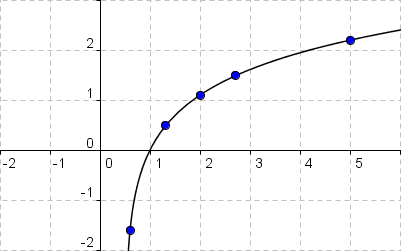
Die nächste Aufgabe lautet die Gleichung der Tangente yt an f im Punkt (1 , f(1)) anzugeben!
Eine Tangente yt=mx+n an den Graphen einer Funktion f in einem Punkt (xo , f(xo) bestimmt man mit der Gleichung yt = f´(xo)·(x – xo) + f(xo).
Es ist hier f(x) = ln(2x-1) und (xo , f(xo) = (1 , 0).
Die Ableitung f´ von f berechnen wir mit Hilfe der Kettenregel (innere Ableitung mal äußere Ableitung):
f´(x) = 2 · 1/(2x-1) , denn (2x-1)´ = 2 und ln´(x) = 1/x.
Damit ist dann f´(1) = 2 · 1/(2·1-1) = 2 · 1 = 2.
Wir erhalten für die gesuchte Tangentengleichung:
yt = f´(xo)·(x – xo) + f(xo)
yt = f´(1)·(x – 1) + f(1)
yt = 2·(x – 1) + 0
also yt = 2x – 2 .
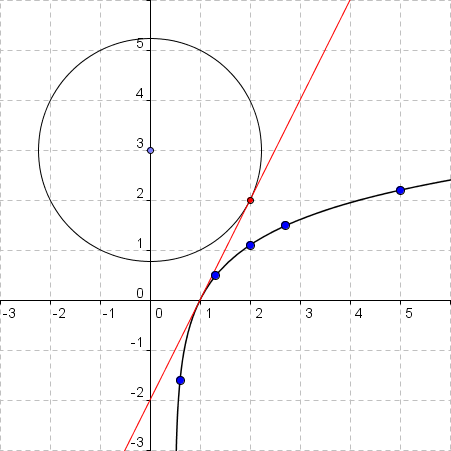
Der Kreis mit Mittelpunkt (0 , 3) und Radius √5 ist in das Koordinatensystem einzuzeichnen und seine Gleichung anzugeben!
Hätte unser Kreis seinen Mittelpunkt im Koordinatenursprung (0 , 0), so kämen wir mit dem Satz des Pythagoras auf die Gleichung
x2 + y2 = 5 .
Unser Mittelpunkt (0 , 3) ist aber gegenüber dem Koordinatenursprung um 3 Einheiten nach oben verschoben. Die gesuchte Kreisgleichung lautet daher
x2 + (y-3)2 = 5 .
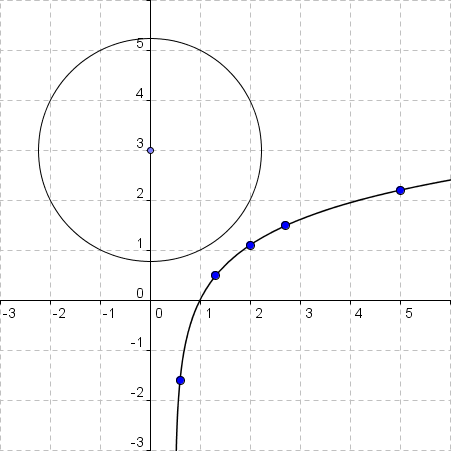
Es ist nun rechnerisch nachzuweisen, dass der Kreis und die Tangente einen gemeinsamen Punkt besitzen und die Koordinaten dieses Punktes sind anzugeben!
Da, wo Kreis und Tangente sich berühren/schneiden gilt
sowohl y = 2x – 2 als auch x2 + (y-3)2 = 5.
Um x und y zu bestimmen, setzen wir zunächst 2x – 2 anstelle von y in die Kreisgleichung ein und eliminieren damit die Variable y:
x2 + (2x – 2 – 3)2 = 5
x2 + (2x – 5)2 = 5
x2 + 4x2 – 20x + 25 = 5
5x2 – 20x + 25 = 5 | -5
5x2 – 20x + 20 = 0 | :5
x2 – 4x + 4 = 0
Diese quadratische Gleichung lösen wir mit der pq-Formel:
x1,2 = -p/2 ± (p2/4 – q)1/2
x1,2 = 2 ± (4 – 4)1/2
x1 = x2 = 2.
Es gibt als genau einen gemeinsamen Punkt bei x=2. Der zugehörige y-Wert dieses Punktes ergibt sich durch Einsetzen von x=2 in die Tangentengleichung und führt auf y=2.
Kreis und Tangente haben also den einen gemeinsamen Punkt (2, 2).