Auf dieser Seite gibt es für euch den zweiten Teil der original Analysis – Mathe Abituraufgaben mit Lösungen – aus Sachsen aus dem Jahre 1994.
Quelle der Aufgaben ist das Buch Abitur 2000, Stark Verlag, ISBN 3-89449-264-3.
Inhalt in Stichwörtern: Natürlicher Logarithmus, Stammfunktion, Fläche berechnen, Parabel, erste und zweite Ableitung, Schnittpunkte berechnen, Abstand, Minimum bestimmen, pq-Formel
Aufgaben mit Lösungen – Teil 2
Wir betrachten erneut die Funktion y = f(x) = ln(2x – 1).
Es ist nachzuweisen, dass die Funktion F(x) = 1/2 (2x – 1) · ln(2x – 1) – x eine Stammfunktion von f ist!
Wir müssen die erste Ableitung von F, also F´ berechnen – und dabei sollte dann f herauskommen, denn eine Funktion F ist Stammfunktion einer Funktion f, wenn F´ = f gilt.
Wir können F in der Form F(x) = u(x)·v(x) – w(x) ausdrücken mit
u(x) = 1/2 (2x – 1)
v(x) = ln(2x – 1)
w(x) = x .
Dann ist F´(x) = [u(x)·v(x)]´ – w´(x). Die Ableitungen von u, v und w sind:
u´(x) = 1
v´(x) = 2/(2x – 1) (Kettenregel: innere Ableitung mal äußere Ableitung)
w´(x) = 1 .
Die Ableitung von u(x)·v(x) ergibt sich mit der Produktregel:
[u(x)·v(x)]´
= u´(x) · v(x) + u(x) · v´(x)
= 1 · ln(2x – 1) + 1/2 (2x – 1) · 2/(2x – 1)
= ln(2x – 1) + 1 .
Damit erhalten wir schließlich
F´(x) = [u(x)·v(x)]´ – w´(x) = ln(2x – 1) + 1 – 1 = ln(2x – 1) = f(x)
und der Nachweis ist erbracht.
Zu berechnen ist nun die Fläche zwischen dem Graphen von f(x) = ln(2x – 1) und der x-Achse über dem Intervall 1≤x≤5 !
Zur Lösung dieser Aufgabe verwenden wir die Stammfunktion F aus der vorigen Aufgabe. Es ist
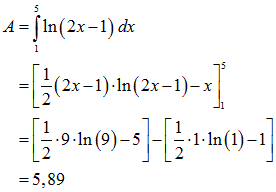
der gesuchte Flächeninhalt.
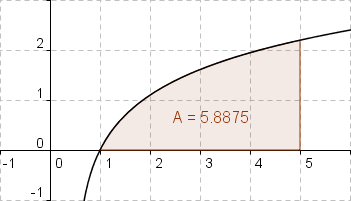
Gesucht ist eine Parabel ga(x) = ax2, sodass der Punkt (0,5 ; 0,5) auf der Parabel liegt!
Um diese Aufgabe zu lösen, setzen wir x=0,5 und ga(x)=0,5 in die Funktionsgleichung ga(x) = ax2 ein und lösen dann nach a auf:
a · 0,52 = 0,5 | : 0,52
a = 0,5 / 0,52 = 1 / 0,5 = 2
Die Parabel g2(x) = 2x2 geht durch den Punkt (0,5 ; 0,5).
Gesucht ist eine Parabel ga(x) = ax2, mit dem Anstieg m=2 an der Stelle x=1,5 !
Um die Parabel zu bestimmen – also das spezielle a zu finden – benötigen wir die erste Ableitung von ga. Diese muss nämlich die Bedingung ga´(1,5) = 2 erfüllen. Es ist
ga´(x) = [ax2]´ = 2ax .
Wir erhalten dann die Gleichung 2 = 2·a·1,5 und daraus mit etwas Umformarbeit a = 2/3. Die gesuchte Parabel lautet damit g2/3(x) = 2/3 x2.
Die nächste Aufgabe besteht darin, die Parabel g1/3(x) = 1/3 x2 zusammen mit der Tangente yt = 2x – 2 von f (aus Teil 1 dieser Abituraufgaben) in ein Koordinatensystem zu zeichnen und die Koordinaten der Schnittpunkte beider Funktionen zu berechnen!
Um die Schnittpunkte zu berechnen, müssen wir die Funktionsterme beider Funktionen einander gleichsetzen und die so entstandene quadratische Gleichung lösen. Dies wird zunächst die Schnittstellen x1 und x2 ergeben:
1/3 x2 = 2x – 2 | – 2x + 2
1/3 x2 – 2x + 2 = 0 | ·3
x2 – 6x + 6 = 0
und mit pq-Formel
x1,2 = -p/2 ± √(p2/4 – q)
x1,2 = 3 ± √(9 – 6) = 3 ± √3
x1 = 4,73
x2 = 1,27
Jetzt setzen wir noch diese beiden Lösungen in die Tangentengleichung ein, um die entsprechenden y-Werte der Schnittpunkte zu berechnen:
y1 = 2·4,73 – 2 = 7,46
y1 = 2·1,27 – 2 = 0,54
Die gesuchten Schnittpunkte lauten somit (4,73 ; 7,46) und (1,27 ; 0,54).
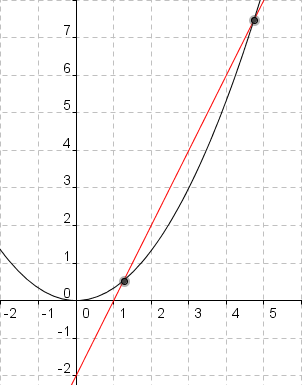
In der letzten Aufgabe des zweiten Teils dieser Analysisaufgaben betrachten wir wieder die Parabel g1/3(x) = 1/3 x2 zusammen mit der Funktion f(x) = ln(2x – 1) und suchen im Intervall 0,5<x<5,0 nach derjenigen Stelle xE, an der der Abstand zwischen g1/3 und f am geringsten ist!
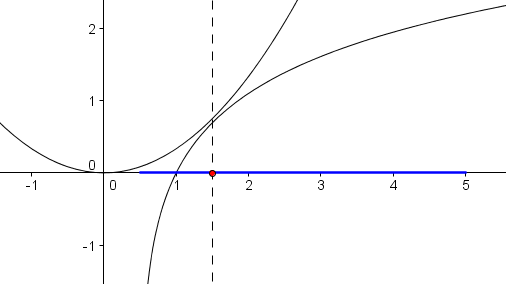
Da der Graph der Parabel oberhalb des Graphen der Logarithmusfunktion liegt, berechnet sich der Abstand d(x) zwischen beiden durch
d(x) = 1/3 x2 – ln(2x – 1) .
Mit Hilfe von Differentialrechnung bestimmen wir nun das Minimum dieser Funktion im Intervall 0,5<x<5,0:
Es ist d´(x) = 2/3 x – 2/(2x – 1) die erste Ableitung von d. Nur die Nullstellen hiervon kommen als Extremstellen der Funktion d in Frage:
2/3 x – 2/(2x – 1) = 0 | ·(2x – 1)
2/3 x·(2x – 1) – 2 = 0
4/3 x2 – 2/3x – 2 = 0 | · 3/4
x2 – 1/2x – 3/2 = 0
Mit der pq-Formel finden wir die Lösungen:
x1,2 = -p/2 ± √(p2/4 – q)
x1,2 = 1/4 ± √(1/16 + 3/2) = 1/4 ± √(25/16)
x1 = 1/4 + 5/4 = 6/4 = 1,5
x2 = 1/4 – 5/4 = -4/4 = -1
Die -1 kommt für unser gesuchtes Minimum nicht in Frage, da sie nicht mehr im betrachteten Intervall liegt. Wir testen also noch, ob tatsächlich bei x = 1,5 ein Minimum der Funktion d vorliegt. Dazu benutzen wir deren zweite Ableitung:
d´´(x) = [2/3 x – 2/(2x – 1)]´ = 2/3 + 4/(2x – 1)2
d´´(1,5) = 2/3 + 4/(2·1,5 – 1)2 = 2/3 + 4/22 = 2/3 + 4/4 > 0
Da die zweite Ableitung von d an der Stelle x = 1,5 größer als Null ist, hat d bei x = 1,5 tatsächlich ein Minimum. Es lautet
d(1,5) = 1/3·1,52 – ln(2·1,5 – 1) = 0,75 – ln(2) = 0,057 .
Der minimale Abstand zwischen g1/3 und f beträgt also 0,057.