In diesem Beispiel ist eine gewisse Fläche zwischen den Graphen der beiden Funktionen f(x) = sin(x) und g(x) = sin(2x) zu berechnen.
Aufgabe:
Die Graphen der Funktionen f(x) = sin(x) und g(x) = sin(2x) haben einen Schnittpunkt S(xs ; f(xs)) mit 0 < xs < π/2.
Wie groß ist die Fläche, die von beiden Graphen über dem Intervall 0 bis xs eingeschlossen wird?
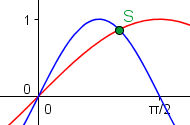
Fläche zwischen sin(x) und sin(2x) gesucht
Hinweise, Lösungsansatz:
Zunächst bestimmt man xs, die Stelle an der sich die beiden Graphen schneiden.
Dafür benutzt man die Beziehung sin(x + y) = cos(y)·sin(x) + cos(x)·sin(y), aus der man
sin(2x) = sin(x + x) = cos(x)·sin(x) + cos(x)·sin(x) erhält.
Wenn dann xs bestimmt ist, geht die Berechnung der Fläche mit Hilfe des bestimmten Integrals
Lösung:
Es ist sin(xs) = sin(2xs) = sin(xs + xs),
weiter sin(xs) = sin(xs)·cos(xs)+cos(xs)·sin(xs),
bzw. 1 = cos(xs) + cos(xs) = 2 cos(xs),
schließlich cos(xs) = 1/2.
Das gesuchte xs erfüllt also die Bedingung
cos(xs) = 1/2 und der Arkuscosinus liefert
xs = π/3 ≈ 1,0472.
Jetzt kann die Fläche berechnet werden:
![A = \int\limits_0^{\pi/3} \sin(2x)-\sin(x) dx = \left[ \cos(x) - \frac{1}{2} \cos(2x) \right]_0^{\pi/3} = 0,25](http://s0.wp.com/latex.php?latex=A+%3D+%5Cint%5Climits_0%5E%7B%5Cpi%2F3%7D+%5Csin%282x%29-%5Csin%28x%29+dx+%3D+%5Cleft%5B+%5Ccos%28x%29+-+%5Cfrac%7B1%7D%7B2%7D+%5Ccos%282x%29+%5Cright%5D_0%5E%7B%5Cpi%2F3%7D+%3D+0%2C25+&bg=ffffff&fg=000000&s=0 "A = \int\limits_0^{\pi/3} \sin(2x)-\sin(x) dx = \left[ \cos(x) - \frac{1}{2} \cos(2x) \right]_0^{\pi/3} = 0,25")
Die betrachtete Fläche zwischen den beiden Funktionsgraphen beträgt 0,25.
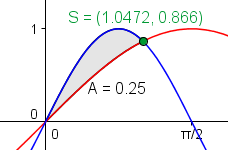
Fläche zwischen sin(x) und sin(2x)
von 0 bis Pi/3