Auf dieser Seite gibt es für euch original Mathe Abituraufgaben mit Lösungen und zwar den Teil B1, Aufgabe a und b – Geometrie/Algebra (Sachsen 1994).
Quelle der Aufgaben ist Abitur 2000 – Prüfungsaufgaben mit Lösungen (ISBN 3-89449-264-3) aus dem STARK Verlag.
Gegeben:
Punkte A = (7; -5; 0) und B = (2; 0; 0) sowie eine Gerade g durch die Gleichung
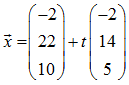
Aufgabe a)
Stelle fest, ob der Punkt C = (2; -6; 0) auf der Geraden g liegt!
Bestimme den Schnittpunkt von g mit der y-z-Ebene!
Lösung:
Wenn C auf g liegt, muss es ein t geben, sodass
2 = -2 + t·(-2)
-6 = 22 + t·14
0 = 10 + t·5
Aus allen drei Gleichungen ergibt sich t = -2, also liegt C auf g.
Der Schnittpunkt (xS; yS; zS) von g mit der y-z-Ebene muss die Bedingung xS = 0 erfüllen. Mit Hilfe der Geradengleichung ergibt sich
0 = -2 + t·(-2) also t = -1.
Mit diesem t können wir yS und zS berechnen:
yS = 22 + (-1)·14 = 22 – 14 = 8
zS = 10 + (-1)·5 = 10 – 5 = 5
Somit ist (0; 8; 5) der Schnittpunkt von g mit der y-z-Ebene.
Aufgabe b)
Warum liegt Dreieck ABC in der x-y-Ebene?
Gesucht ist der Winkel α sowie der Flächeninhalt A des Dreiecks ABC!
Lösung:
Das Dreieck ABC muss in der x-y-Ebene liegen, da bei allen drei Punkten A, B, und C die z-Koordinate gleich Null ist.
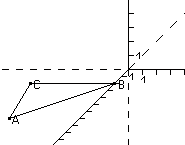
Aus den drei Punkten
A = (7; -5; 0)
B = (2; 0; 0)
C = (2; -6; 0)
ergibt sich das folgende Dreieck:
Der Vektor →
c = →
AB mit der Länge c und Vektor →
b = →
AC mit der Länge b schließen den gesuchten Winkel α ein. Mit Hilfe des Skalarproduktes aus diesen beiden Vektoren ergibt sich:
cos α = →
c · →
b / (c·b)
Es ist
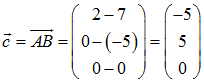
mit einer Länge von c = √((-5)2 + 52 + 02) = √50 und
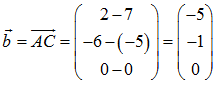
mit einer Länge von b = √((-5)2 + (-1)2 + 02) = √26 .
Damit ergibt sich für α
α = cos-1( 20 / (√50·√26) ) = 56,3° .
Der Flächeninhalt des besagten Dreiecks ist A = 0.5 · c · b · sin α, also
A = 0.5 · √50 · √26 · sin 56,3° = 15 .