Auf dieser Seite gibt es für euch Geometrie/Algebra – Mathe Abituraufgaben mit Lösungen und zwar den Teil B1, Aufgabe e und f (Sachsen 1994).
Gegeben:
Punkte
A = (7; -5; 0)
B = (2; 0; 0)
C = (2; -6; 0)
D = (0; 8; 5)
Fläche des Dreiecks ABC
AABC = 15
sowie der zugehörige Umkreis k dieses Dreiecks durch die Gleichung (x – 4)2 + (y + 3)2 = 13
mit Mittelpunkt M = (4; -3; 0)
Aufgabe e)
Gesucht ist das Volumen der Pyramide mit der dreieckigen Grundfläche ABC und der Spitze D!
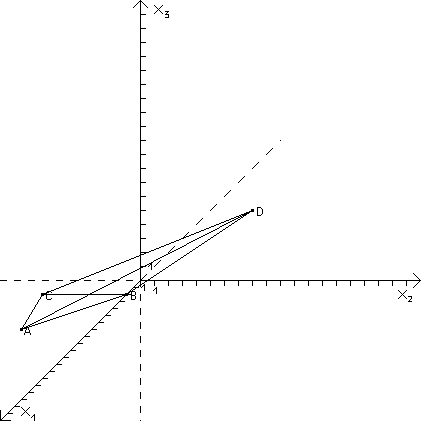
Gesucht ist weiterhin das Volumen des Kreiskegels, dessen Grundfläche der Fläche des Kreises k entspricht und der ebenfalls die Spitze D hat!
In welchem Verhältnis steht das Volumen des Kreiskegels zum Volumen der Pyramide?
Lösung:
Das Volumen einer Pyramide berechnet sich nach der Formel
V = 1/3 x Grundfläche x Höhe.
Dabei spielt es keine Rolle, dass diese Pyramide hier schief ist. Die Grundfläche ist gegeben – genau wie die Höhe. Die Höhe ist nämlich der Abstand der Spitze D von der x-y-Ebene, in welcher die Grundfläche der Pyramide liegt. Da der Punkt D = (0; 8; 5) die z-Koordinate 5 hat, ist das also die besagte Höhe.
Wir erhalten für das Pyramiden-Volumen VP = 1/3 · 15 · 5 = 25.
Auch das Volumen des Kreiskegels berechnet sich nach der Formel
V = 1/3 x Grundfläche x Höhe.
Die Grundfläche ist hier aber ein Kreis, d.h. man rechnet für die Fläche π r2, wobei r2 = 13 ist, wie aus der gegebenen Kreisgleichung hervorgeht.
Wir erhalten für das Kreiskegel-Volumen VK = 1/3 · π·13 · 5 = 68,1.
Das gesuchte Verhältnis der Volumina lautet VK / VP = 68,1 / 25 = 2,72.
Aufgabe f)
Man betrachte irgendeinen Punkt S, der nicht in der x-y-Ebene liegt und wie in Aufgabe e) die Spitze eines Kreiskegels mit der Fläche des Kreises k und gleichzeitig Spitze der darin enthaltenden Pyramide mit der Fläche des Dreiecks ABC ist.
Es ist zu zeigen, dass das Verhältnis von Kreiskegelvolumen VK zu Pyramidenvolumen VP nicht vom Punkt S = (xS; yS; zS) abhängt!
Lösung:
Für den Nachweis benutzen wir die beiden Volumenformeln für Kreiskegel und Pyramide:
VK = 1/3 · AKreis · h und VP = 1/3 · ADreieck · h
In beiden Formeln kommt die gleiche Höhe h = zS (die z-Koordinate von Punkt S) vor. Teilen wir nun VK durch VP, so erhalten wir (da sich 1/3 und zS herauskürzen)
AKreis / ADreieck = π·13 / 15 = 2,72
also das gleiche Verhältnis wie in der vorigen Aufgabe, wobei bei dessen Berechnung der Punkt S keine Rolle spielte.
Quelle: Die Aufgaben sind dem Buch Abitur 2000 – Prüfungsaufgaben mit Lösungen, STARK Verlag, 1999 entnommen.